2,5
Объяснение:
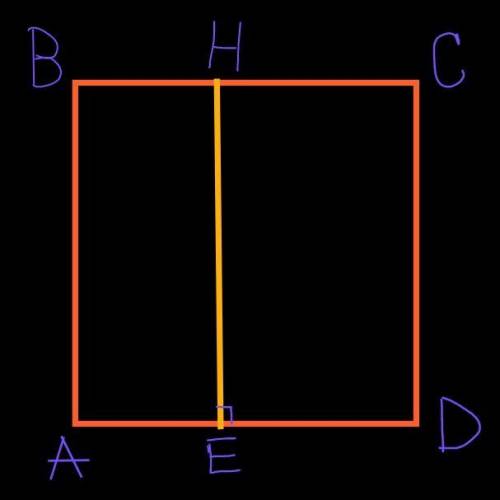
Назовём точки как на рисунке.
Пусть периметр прямоугольника АВНЕ равен 7.
P(прямоугольника)=(а+б)*2,
где а и б стороны прямоугольника. Следовательно а+б=P÷2; тоесть АВ+АЕ=7÷2; АВ+АЕ=3,5
Пусть периметр прямоугольника CDEH равен 8.
P(прямоугольника)=(а+б)*2,
где а и б стороны прямоугольника
Следовательно а+б=P÷2; тоесть CD+DE=8÷2; CD+DE=4.
АЕ+DE=AD. Тогда АВ+АD+CD=3,5+4=7,5.
АВ, AD и CD – стороны квадрата ABCD
Все стороны квадрата равны, следовательно одна сторона равна 7,5÷3=2,5
ответ: 2,5
2,5
Объяснение:
Назовём точки как на рисунке.
Пусть периметр прямоугольника АВНЕ равен 7.
P(прямоугольника)=(а+б)*2,
где а и б стороны прямоугольника. Следовательно а+б=P÷2; тоесть АВ+АЕ=7÷2; АВ+АЕ=3,5
Пусть периметр прямоугольника CDEH равен 8.
P(прямоугольника)=(а+б)*2,
где а и б стороны прямоугольника
Следовательно а+б=P÷2; тоесть CD+DE=8÷2; CD+DE=4.
АЕ+DE=AD. Тогда АВ+АD+CD=3,5+4=7,5.
АВ, AD и CD – стороны квадрата ABCD
Все стороны квадрата равны, следовательно одна сторона равна 7,5÷3=2,5
ответ: 2,5

28,5
Объяснение:
Пусть стороны = x, y и z
Раз р/б треуг. следовательно какие-то две стороны равны. Пусть x и y. В условии две разных суммы, то есть не может быть такого что x+z=16, y+z=25 (т.к. мы предположили что x и y равны). Значит x (ну либо y)+z=16 и x+y=25 либо же наоборот (первая сумма=25, вторая=16). Следовательно в первом случае (т.к. x=y и при этом их сумма 25) x=y=12,5 следовательно периметр=16+12,5=28,5. Второй случай:x=y=8 следовательно периметр=8+25=33 но этот вариант не подходит из-за неравенства сторон треугольника, т.к. z получается=17 и это больше чем сумма двух других сторон (16).