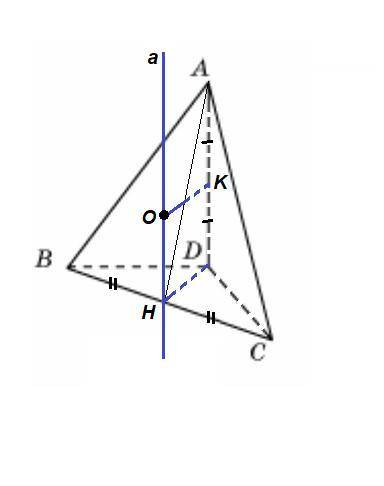
1) Через середину гипотенузы строим прямую а, перпендикулярную основанию.
2) В плоскости, которая задается этой прямой и ребром AD проводим серединный перпендикуляр к AD.
3) Точка пересечения серединного перпендикуляра и прямой а - центр описанной сферы.
Объяснение:
Если сфера описана около данной пирамиды, то основание пирамиды вписано в окружность - сечение сферы.
Основание - прямоугольный треугольник. Центр описанной около него окружности лежит на середине гипотенузы.
Пусть Н - середина гипотенузы ВС прямоугольного треугольника BCD.
Тогда точка Н - центр окружности, описанной около ΔBCD, равноудалена от всех вершин основания.
Отрезок, соединяющий центр сечения сферы с центром сферы, перпендикулярен сечению.Проведем через точку Н прямую а║AD. AD⊥(BCD), так как AD⊥BD и AD⊥DC, значит а⊥(BCD).
Центр сферы будет лежать на прямой а.
Любая точка прямой а равноудалена от вершин основания. Осталось найти на ней точку, удаленную от вершины А на то же расстояние, что и от остальных вершин.
Для этого в плоскости (ADH) проведем серединный перпендикуляр к ребру AD. К - середина AD, проведем КО║DН до пересечения с прямой а.
О - центр сферы.
Объяснение:
h= 4 см
d= 6 cм
Sбок.-?
Найдем радиус r=d /2= 6/2=3 см
l - образующая конуса, ее длину мы пока не знаем.
Образующую l можно найти по теореме Пифагора:
l^2 =h^2 + r^2.
l^2 =4^2+ 3^2
l^2 = 25.
l = 5 (см).
Воспользуемся формулой для вычисления площади боковой поверхности конуса:
S бок. = πRL.
Подставим известные нам данные в формулу и получим:
S бок. = π х 3 х 5 = 15 π (см2).