РЕШЕНИЕ ПРИЛОЖЕНО
###################
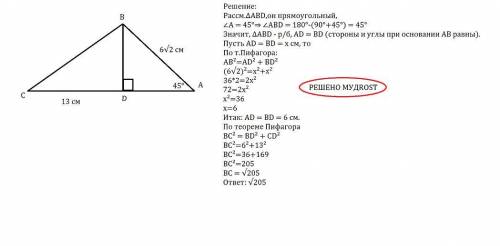
РА - перпендикуляр к площади параллелограмма АВСД. Укажите вид параллелограмма, если РВ перпендикулярен ВС. а) ромб, б) прямоугольник; в) квадрат.
Объяснение: РВ - наклонная. АВ - её проекция на плоскость АВСД. По т. о 3-х перпендикулярах если наклонная (РВ) перпендикулярна прямой (ВС) на плоскости, то её проекция на ту же плоскость перпендикулярна данной прямой. Следовательно, АВ⊥ВС, и угол АВС - прямой. Противоположные углы параллелограмма равны. ⇒ ∠Д=∠В=90°, поэтому из суммы углов четырехугольника ∠А+∠С=360°-2•90°=180°, и каждый из них равен 180°:2=90°.
Углы четырехугольника АВСД прямые. ⇒ АВСД - прямоугольник. Он может быть и квадратом. если его стороны будут равны.
√205 см
Объяснение:
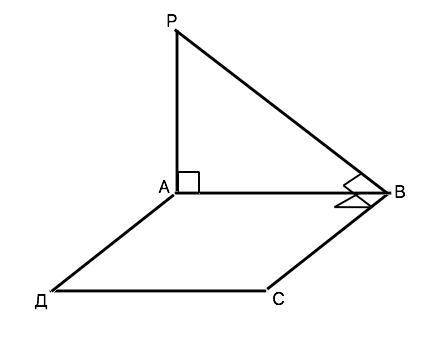
Розглянемо ΔАВD - прямокутний, ∠А=45°, отже, ∠АВD=90-45=45°, а ΔАВD - рівнобедрений, АD=ВD.
Нехай АD=ВD=х см, тоді за теоремою Піфагора
АD²+ВD²=АВ²; 2х²=72; х²=36; х=6; АD=ВD=6 см.
За теоремою Піфагора
ВС²=ВD²+СD²=36+169=205; ВС=√205 см