Объяснение:
Имеем угол α = 60°, который образует луч OA с положительной полуосью Ox. Длина отрезка OA = 54. Определи координаты точки A."
Длина отрезка в координатной плоскости определяют по формуле:
Катет, лежащий против угла в 30* равен 1/2 гипотенузы.
ОхА=(1/2)*54=27.
По теореме Пифагора ОуА²=ОА²-ОхА²=54²-27²=2916-729=2187.
ОуА=27√3.
На украинском:
Довжина відрізка в координатній площині визначають за формулою: Катет, що лежить проти кута в 30 * дорівнює 1/2 гіпотенузи. ОхА=(1/2) * 54=27. За теоремою Піфагора ОуА2=ОА2-ОхА2=542-272=2916-729=2187. ОуА=27√3.
Описанная трапеция - это трапеция, в которую вписана окружность. ЕЕ можно вписать в трапецию ТОЛЬКО ТОГДА, когда сумма оснований трапеции равна сумме боковых сторон. Пусть три последовательные стороны трапеции равны 2х, 7х и 12х. Тогда ясно, что две противоположные стороны - это стороны 2х и 12х и их сумма равна 14х. значит четвертая сторона этой трапеции тоже равна 7х, так как 2+12=14 и 7+7=14. Периметр равен 28х и равен 42. Тогда х= 42:28 = 3/2 см. Стороны трапеции равны 2х=3 см; 7х=10,5 см; 12х=18 см и 7х=10,5 см.
ответ: стороны трапеции 3см, 10,5см, 18см и 10,5 см.
Проверка: 3+10,5+18+10,5 =42
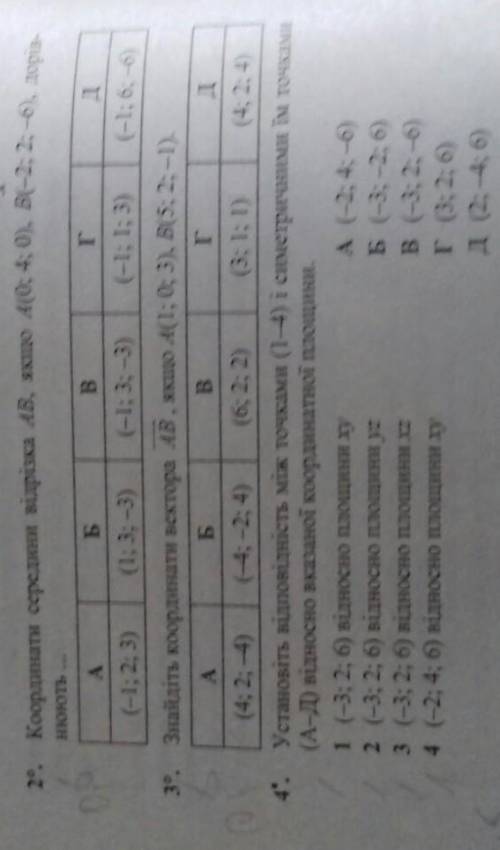
1) (-1;3;-3)В 2) (4;2;-1) А 3) 1-В, 2-Г, 3-Б, 4-А
Объяснение: