Цилиндр описан около сферы.
R цилиндра = 2 см.
Найти:S полн поверхности цилиндра - S полностью поверхности сферы = ?
Решение:Так как в данный цилиндр вписана сфера, по условию ⇒ D сферы = h цилиндра.
R цилиндра = R сферы = 2 см (так как в цилиндр вписана сфера).
⇒ D сферы = h цилиндра = R сферы * 2 = 2 * 2 = 4 см.
S полн поверхности цилиндра = 2πR(R + h), где R - радиус цилиндра; h - высота цилиндра.
S полн поверхности цилиндра = π(2 * 2(2 + 4) = 24π см²
S полной поверхности сферы = 2πR² , где R - радиус сферы.
S полной поверхности сферы = π(4 * 2²) = 16π см²
⇒S полн поверхности цилиндра - S полн поверхности сферы = 24 - 16 = 8π см²
ответ: 8π см²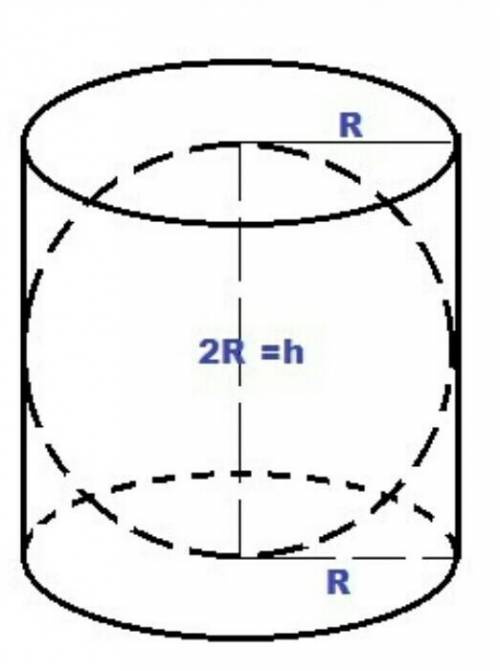
Для того, чтобы четырехугольник мог быть вписан в окружность, необходимо и достаточно, чтобы суммы его противоположных сторон были равны. Обозначим 1 часть за x, тогда:
1). Стороны четырехугольника равны 7x, 3x, 2x, 6x в порядке следования, а суммы противоположных сторон равны:
7x+2x=3x+6x => 9x=9x, верно, значит такой четырехугольник может быть вписан в окружность.
2). Стороны четырехугольника равны 5x, 4x, 3x, 6x в порядке следования, а суммы противоположных сторон равны:
5x+3x=4x+6x => 8x≠10x, неверно, значит такой четырехугольник не может быть вписан в окружность.
ответ: 1). Да, может; 2). Нет, не может.
Різниця між поверхнями циліндра і кулі буде 8πr²
Объяснение S пов=S основ+S бок=2πr²+2πr*2r=4πr²+8π=12πr²
Площа кулі буде 4πr² тоді різниця буде 12πr²-4πr²=8πr²