Объяснение:
Сторона правильного шестиугольника равна радиусу описанной окружности. Следовательно сторона а основания равна 2 ед. Боковая сторона правильной шестиугольной пирамиды состоит из шести равнобедренных треугольников с основанием а=2. Проведем высоту в основании и найдем её по т.Пифагора. h=√(2²-1²)=√3 ед. Плоскость боковой стороны наклонена под углом 30°, следовательно угол между высотой пирамиды и высотой боковой грани - 30°. Высота пирамиды, высота грани и высота треугольника основания - прямоугольный треугольник с гипотенузой - высота боковой грани и катетами - высота пирамиды - Н и высота треугольника основания - √3. По свойству катета лежащего против угла 30° составляем уравнение:
(2Н)²=(√3)²+Н², где Н - высота пирамиды;
3Н²=3
Н=1 ед;
тогда апофема равна - 2Н=2 ед;
Р=6*2=12 ед;
S=12*2*1/2=12 ед².
1) CB = AB = 8, AC = 8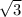
, <A = <C = 30 <B = 120
2) 400 * sin113 * sin53 / sin14
3) AC =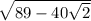 
<A = Arccos( (AC^2 + AB^2 -BC^2)/2AC*AB )
<B = Arccos( (BC^2 + AB^2 -AC^2)/2BC*AB )
Если нужно найти приближенное целочисленное значение нужно подставить и посчитать на калькуляторе
Объяснение:
1) <C = 180-120-30 = 30 значит треугольник ABC равнобедренный с основанием AC. CB = AB = 8. Пусть BD высота, она же медиана.
<DBA = 120 / 2 = 60. AD = AB * sin<DBA = 8* 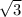/2 = 4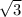
AC = 2AD = 8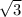
2) BC = AC * sinA / sinB
S = AC * BC * sinC / 2 = 20* 20 * sin113 * sin53 / sin14
3) AC = 
так как все стороный найдены можно подставить их значения в формулы:
<A = Arccos( (AC^2 + AB^2 -BC^2)/2AC*AB )
<B = Arccos( (BC^2 + AB^2 -AC^2)/2BC*AB )
Если нужно найти приближенное целочисленное значение нужно подставить и посчитать на калькуляторе
Найти: d
По основному тригонометрическому свойству:
cos²(BAO)+sin²(BAO)=1
(0,6)²+sin²(BAO)=1
sin²(BAO)=0,64
Совокупность:
sin(BAO)=0,8
sin(BAO)=–0,8
Так как угол ВАО меньше 180°, то sin(BAO)=0,8
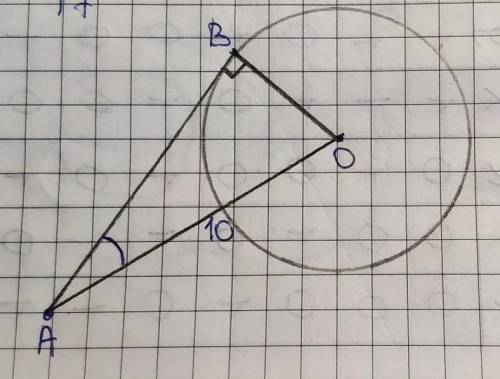
Проведем ОВ.
ОВ перпендикулярен АВ, так как радиус окружности, проведенный к точке касания касательной, перпендикулярен этой касательной.
То есть угол ОВА=90°, а ∆ОВА – прямоугольный.
В прямоугольном ∆ВАО:
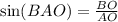
Подставим известные значения:
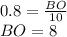
ВО – радиус окружности.
Диаметр вдвое больше радиуса, следовательно d=BO*2=8*2=16 см.
ответ: 16 см.
12 см²
Объяснение:
Шестиугольник образован из 6 равносторонних треугольников сторона треугольника равна радиусу.
а=R=2 cm
Найдем высоту треугольника по формуле
h=а√3/2
h=2√3/2=√3 высота треугольника
Найдем апофему пирамиды.
cos30°=h/H
cos30°=√3/2
√3/2=√3/H
H=2√3/√3
H=2cm апофема пирамиды.
Р=6*а=6*2=12 см периметр шестиугольника
S=1/2РH=1/2*12*2=12 см² площадь боковой поверхности пирамиды