Как схематически набросить график x^2/25-y^2/16=1 Там нужны асимптоты в основном И в центре еще вроде какой-то прямоугольник получается (но это не точно)
Это гипербола с большей полуосью и меньшей полуосью .
Асимптоты гиперболы:
Изобразить асимптоты и график может прямоугольник размера со сторонами, параллельными осям координат, проходящий через точки . Асимптоты проходят через противоположные вершины прямоугольника.
Сам график касается этого прямоугольника в точках , то есть в точках . Далее график приближается к асимптотам. Для более точного построения можно просчитать пару точек.
Биссектрисы смежных углов перпендикулярны. [Сумма смежных углов равна 180°; угол между биссектрисами смежных углов равен полусумме смежных углов, т.е. 90°.] ∠A1AO=∠A1BO=90°
Диагонали ромба пересекаются под прямым углом. ∠AOB=90°
Если у четырехугольника три угла прямые, то он является прямоугольником. [Сумма углов четырехугольника равна 360°; 360°-90°·3=90°; четырехугольник, у которого противоположные углы равны, является параллелограммом; параллелограмм, у которого (хотя бы) один угол прямой, является прямоугольником.] ∠AA1B=90°
Вписываем в исходный треугольник окружность с центром О, проводим касательные перпендикулярно биссектрисам двух острых углов исходного треугольника (на рисунке ST и UV). Эти касательные отрезают два остроугольных треугольника AST и UVC (т.к равнобедренные треугольники с острым углом противолежащим основанию являются остроугольными). В центральном 5-угольнике все его внутренние углы тупые (кроме, может быть угла B). Соединяем вершины этого 5-угольника с центром О. Полученные пять треугольников остроугольные, потому что проведенные отрезки - биссектрисы углов 5-угольника, а биссектрисы делят любой угол на два острых, причем, если угол был тупой, то его половина больше 45 градусов, т.е. это означает что углы при вершине О, острые.
P.S. Можно доказать, что меньше, чем на 7 остроугольных треугольников разрезать нельзя.
Это гипербола с большей полуосью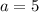 и меньшей полуосью
и меньшей полуосью 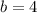 .
.
Асимптоты гиперболы: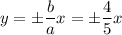
Изобразить асимптоты и график может прямоугольник размера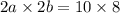 со сторонами, параллельными осям координат, проходящий через точки
со сторонами, параллельными осям координат, проходящий через точки 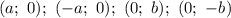 . Асимптоты проходят через противоположные вершины прямоугольника.
. Асимптоты проходят через противоположные вершины прямоугольника.
Сам график касается этого прямоугольника в точках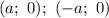 , то есть в точках
, то есть в точках 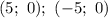 . Далее график приближается к асимптотам. Для более точного построения можно просчитать пару точек.
. Далее график приближается к асимптотам. Для более точного построения можно просчитать пару точек.