
2. S=1/2*6*8=24 см²
чтобы найти периметр,надо найти сторону. находим по теореме Пифагора:
√(1/2*6)²+(1/2*8)²=5
Р=5*4=20 см
4. При пересечении двух хорд произведение длин отрезков, образованных точкой пересечения, одной хорды, равно произведению длин отрезков другой хорды.
АМ * ВМ = СМ * ДМ.
Пусть длина отрезка СМ = Х см, тогда ДМ = (23 – Х) см.
12 * 10 = Х * (23 – Х).
120 = 23 * Х – Х2.
Х2 – 23 * Х + 120 = 0.
Решим квадратное уравнение.
Х1 = 8 см.
Х2 = 15 см.
Если СМ = 8 см, ДМ = 15 см.
Если СМ = 15 см, ДМ = 8 см.
ответ: Длины отрезков равны 8 и 15 см
5. если в окружность вписан прямоугольный треугольник, то его гипотенуза-это диагональ этой окружности, внашем случае она равна 6,5*2=13. по теореме пифагора найдем неизветсный катет, он равен:
корень из гипотенуза квадрате минус другой катет в квадрате, это равно 13*13-5*5=12
площадь треугольника это половина произведения катетов, то есть 0,5*5*12=30
ответ: 30
Объяснение:
1 фото - 1 номер
2 фото - 3 номер
ответ, проверенный экспертом
4,3/5
14
Andr1806
профессор
4.5 тыс. ответов
27.3 млн пользователей, получивших
Поскольку размеров параллелепипеда не дано, будем искать соотношение объемов указанных фигур. Объем параллелепипеда равен произведению площади его основания на высоту.
Объём пирамиды равен: (1/3)*So*h, где So - площадь основания, а h -высота пирамиды. Мы видим, что высота у обеих фигур одна и та же, а площадь основания пирамиды равна половине площади основания параллелепипеда (так как диагональ основания - параллелограмма делит его площадь пополам). Исходя из этого: Vтп/Vпар = [(1/3)*(So/2)*h]/So*h = 1/6, где Vтп - объем треугольной пирамиды, Vпар - объем параллелепипеда, So - площадь основания параллелограмма, h - высота фигур.
Тогда Sтп=Sпар/6. В нашем случае объем треугольной пирамиды будет равен 18/6= 3.
ответ: Vтп=3.
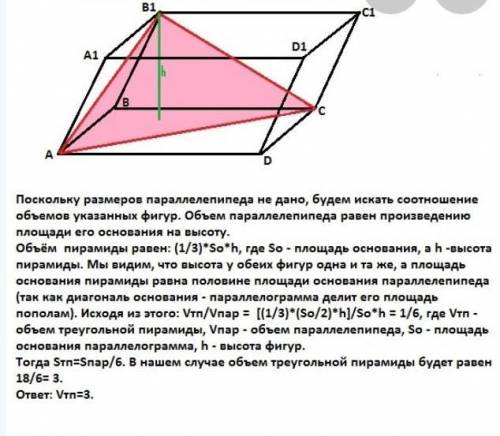
№1 первый рисунок, на нем изображено то что дано.
Так как АВСD – параллелограмм, то АВ||CD, тогда угол DCN = угол
BNC как накрест-лежащие при паралельных прямых AB u CD и секущей CN.
CN – биссектриса по условию, значит угол DCN= угол BCN.
Исходя из равенств: угол BNC= угол DCN= угол BCN. Получим что ∆BNC – равнобедренный с основанием CN, так как углы при его основании равны.
У равнобедренного треугольника боковые стороны равны, следовательно BC=BN=4 см
Периметр параллелограмма это сумма двух его смежных сторон, умноженная на два. Тоесть:
P=(ВС+АВ)*2= (ВС+AN+BN)*2= (4+3+4)*2=22 см.
ответ: 22 см
№2 второй рисунок, на нем изображено то что дано
Та что е ABCD – параллелограмм, то АD||BC, тогда угол DAM= угол BMA как накрест-лежащие при паралельных прямых AD и BC и секущей АМ.
АМ – по условию биссектриса, значит угол DAM= угол BAM.
Исходя из ранее найденного: угол DAM= угол АМВ= угол ВАМ.
Тогда получим что, ∆ВАМ – равнобедренный с основанием АМ, так как углы при основании равны.
АВ=ВМ как боковые стороны равнобедренного треугольника, тогда АВ=5 см.
Периметр параллелограмма это сумма двух его смежных сторон, умноженная на два. Тоесть:
Р=(АВ+ВС)*2=(АВ+ВМ+СМ)*2= (5+5+6)*2= 32 см.
ответ: 32 см