Объяснение:
1) рассмотрим случай когда BE=5cм ; CE=6см
BC=5+6=11cм
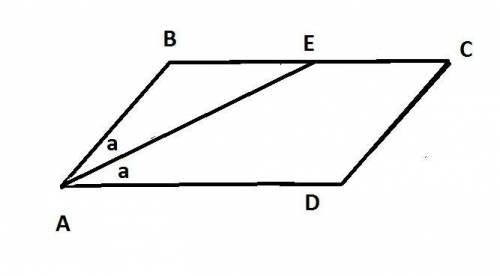
Обозначим ∠BAE=a тогда ∠ЕAD=a так как АЕ - биссектриса и А=2a
сумма углов параллелограмма прилежащих к одной стороне=180°
A+B=180°; B=180°-A=180°-2a
рассмотрим ΔАВЕ
сумма углов треугольника =180°
∠BAE+∠B+∠BEA=180°
∠BEA=180°-∠BAE-∠B=180°-a-(180°-2a)=180°-a-180°+2a=a
∠BEA=a и ∠BAE=a
если в треугольнике два угла равны то он является равнобедренным, а сторона к которой прилежат два равных угла является основанием
⇒ ΔАВЕ-равнобедренный AB=BE=5 см
BC=11cм ; AB=5см
в параллелограмме противоположные стороны равны
тогда периметр Р=2(АВ+BC)=2(5+11)=2*16=32 cм
Р=32 см
2) рассмотрим случай когда BE=6cм ; CE=5см
тогда АВ=BE=6cм
Р=2(АВ+BC)=2(6+11)=2*17=34 cм
Р=34 см
Відповідь:
1) V = π * R² * H
2) V = 1/3 * π * R² * H
3) V = 3/4 * π * R³
4) V = 2/3 * π * R² * H
5) V = 1/3 * π * H² * ( 3 * R - H )
Пояснення:
1) Объем цилиндра с радиусом основания R и высотой H
V = π * R² * H
2) Объем конуса с радиусом основания R и высотой H
V = 1/3 * π * R² * H
3) Объем шара радиуса R
V = 3/4 * π * R³
4) Объем шарового сектора с высотой соответствующего сегмента H и радиусом шара R
V = 2/3 * π * R² * H
5) Объем шарового сегмента высотой H и радиусом шара R
V = 1/3 * π * H² * ( 3 * R - H )
Получается равнобедренный треугольник ABE, так как углы AEB = ABE получаются равными, так как ABE = (AEB = EBC - накрестлежащие при паралелльных прямых). Значит AB = 8
Тогда P = 2* (8+10) = 36