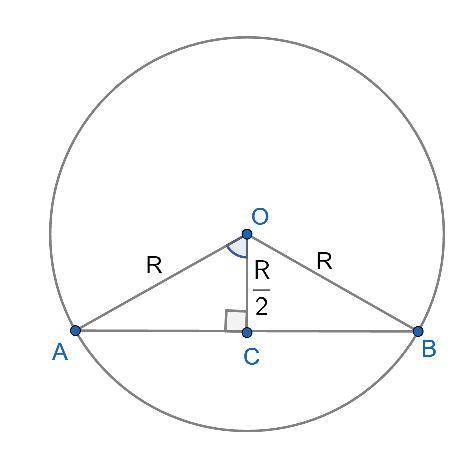
угол АОВ=60°+60°=120°........................
Пусть катеты равны а и b, гипотенуза равна с и высота, проведённая из вершины прямого угла, равна h.
Высота прямоугольного треугольника, проведённая из вершина прямого угла к гипотенузе, равна произведению катетов, делённому на гипотенузу прямоугольного треугольника.Гипотенузу треугольника найдём по теореме Пифагора (сумма квадратов катетов равна квадрату гипотенузы) :
c² = a² + b² = 5² + 12² = 25 + 144 = 169
c = √c² = √169 = 13 см.
Тогда, по выше сказанному, h равно :
h = ab / c = 5 см*12 см / 13 см = 60 см²/13 см = 4 8/13 см.
4 8/13 см.
∠AOB = 120°.
Объяснение:
Рисунок прилагается.
ΔAOB равнобедренный, так как AO = OB = R.
По условию т.C - середина радиуса ⇒ OC = R/2
По условию AB ⊥ OC.
В равнобедренном ΔAOB перпендикуляр ОС является высотой, медианой и биссектрисой.
Тогда ∠AOC = ∠AOB/2;
ΔAOC прямоугольный, ∠ACO = 90°, AO - гипотенуза, OC и AС катеты.
Косинус угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе.
∠AOB = 2 * ∠AOC = 2 * 60° = 120°.