Question

РЕБЯТА две вершины правильного треугольника лежат на оси абцисс, а третья - на оси ординат. Найдите длину стороны треугольника если сумма всех координат всех его вершин равна 2 под корнем 3​

Answer 1

ответ:  а=4 .

ΔАВС - правильный  ⇒  все его стороны равны "а" . Высота равностороннего треугольника является и медианой. Так как ОХ⊥ОУ , то если две вершины лежат на оси ОХ, тогда третья вершина лежит на оси ОУ.  Пусть вершины А и С лежат на оси ОХ, тогда координаты точки А(х,0) , а координаты точки С(-х,0). Вершина В лежит на оси ОУ и её координаты будут В(0,у) .

По условию сумма всех координат равна:  

(-х+0)+(х+0)+(0+у)=2√3  ⇒

у=2√3   (2√3>0  ⇒  точка В лежит в верхней полуплоскости)   ⇒   высота ВО=h=2√3 .

По теореме Пифагора из прямоугольного ΔАВО имеем: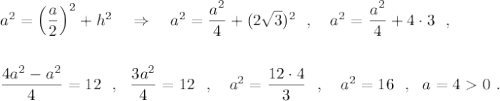   $a^2=\Big(\dfrac{a}{2}\Big)^2+h^2\ \ \ \Rightarrow \ \ \ a^2=\dfrac{a^2}{4}+(2\sqrt3)^2\ \ ,\ \ \ a^2=\dfrac{a^2}{4}+4\cdot 3\ \ ,\\\\\\\dfrac{4a^2-a^2}{4}=12\ \ ,\ \ \dfrac{3a^2}{4}=12\ \ ,\ \ \ a^2=\dfrac{12\cdot 4}{3}\ \ ,\ \ \ a^2=16\ \ ,\ \ a=40\ .$

Длина сторона правильного треугольника равна 4 .