рассмотрим два случая.
1. когда точка касания окружности , вписанной в равнобедренный треугольник , делит одну из боковых сторон на отрезки , равные 30 см и 50см , считая от основания. Тогда радиус найдем как площадь треугольника деленная на полупериметр треугольника.
Если провести касательные к одной окружности, из одной точки, то до точек касания расстояния равны. основание равно 30+30=60/см/, две боковые стороны по 30+50=80/см/, полупериметр равен (2*80+60)/2=80+30=110/см/, площадь равна половине произведения основания на высоту, которую ищем по теореме Пифагора.
√(80²-30²)=√(110*50)=10√55, площадь 10√55*30=300√55, радиус равен 300√55/110≈20.23/см/
2.когда точка касания окружности , вписанной в равнобедренный треугольник , делит одну из боковых сторон на отрезки , равные 30 см и 50см , считая от вершины. Рассуждая аналогично, получим, что
основание равно 50+50=100/см/, две боковые стороны по 30+50=80/см/, полупериметр равен (2*80+2*50)/2=80+50=130/см/, высоту ищем по теореме Пифагора.
√(80²-50²)=√(130*30)=10√39, площадь 50*10√39=500√39, радиус равен 500√39/130≈24.02/см/
Других случаев не вижу, из этих двух наибольшая возможная величина радиуса окружности равна 24.02см
Үшбұрыштың теңдік белгілері.
1. Егер бірінші үшбұрыштың екі қабырғасы мен олардың арасындағы бұрышы екінші үшбұрыштың сәйкес екі қабырғасы мен арасындағы бұрышқа тең болса, онда бұл үшбұрыштар тең болады.
2. Егер бірінші үшбұрыштың бір қабырғасы және оған іргелес жатқан екі бұрышы екінші үшбұрыштың сәйкес қабырғасы мен оған іргелес жатқан екі бұрышына тең болса, онда бұл үшбұрыштар тең болады.
3. Егер бір үшбұрыштың үш қабырғасы екінші үшбұрыштың сәйкес үш қабырғасына тең болса, онда бұл үшбұрыштар тең болады.
Объяснение:
Общее уравнение окружности имеет вид:
(x – a)²+(y – b)²=r²
где a и b – координаты х и у центра окружности соответственно.
Получим:
(х–3)²+(у–2)²=r²
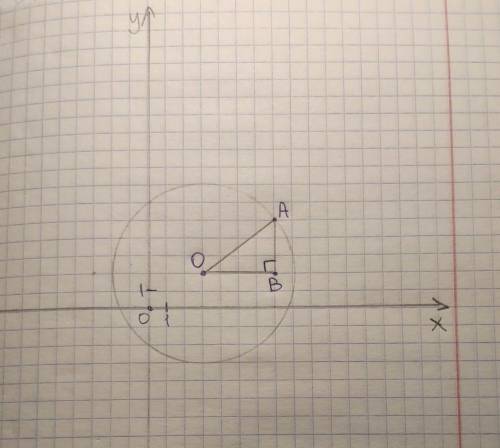
Найдем r. Радиус – это расстояние от центра (пусть это будет точка О) до любой точки на окружности (пусть данная в условии точка будет точка А)
Тогда АО=r; AO²=r².
Проведём из точки А прямую паралельную оси Оу, проведём прямую из точки О паралельную оси Ох. Точка пересечения будет точка В.
Так как кординатные оси перпендикулярны, тоесть образуют угол в 90°, то угол АВО так же будет равен 90°. Тогда ∆АВО – прямоугольный.
В прямоугольном треугольнике АВО по теореме Пифагора:
АО²=АВ²+ВО²
АО²=(5–2)²+(7–3)²
АО²=9+16
АО²=25
Тогда получим:
(х–3)²+(у–2)²=25
ответ: (х–3)²+(у–2)²=25
Объяснение:
к сожалению, дана точка касания, и благодаря этому, мы сможем найти радиус окружности:
1) Мы знаем, что отрезки касательных, проведенных из одной точки, равны =>
Обзовем треугольник, треугольником ABC, где AB=BC и точки касания F, L, K: AF=AK=50; FB=BL= 30; LC=CK=50 => боковые стороны AB и BC = 50+30 = 80, а основание равно AC = 50+50=100
БИНГО! - у нас есть р/б треугольник и мы о нём почти всё теперь знаем. Ну разве не прекрасно ли это?
2) Теперь нам захотелось найти радиус
он находится по формуле:
где
подставляем:
p=80+100/2= 130
r= √(50*50*30/130) ≈ 24,0192230....
Ну, мы случайно нашли радиус этой самой окружности. Наверное, уж точно больше чем 24,0192230.... она быть не может.
- ахх, хочется плакать