Даны вершины А(-7;2) B(5;-3) C(8:1) треугольника АBC.
Составить уравнение высоты, проведенной из вершины С.
Высота СД - это перпендикуляр к прямой АВ.
Составим уравнение прямой АВ.
Вектор АВ = (5-(-7); -3-2) = (12; -5).
Уравнение АВ:
(x + 7)/12 = (y – 2)/(-5) в каноническом виде или
5х + 12у + 11 = 0 в общем виде.
Перпендикулярная прямая в общем виде Ах + Ву + С = 0 имеет коэффициенты по сравнению с АВ, равные В и -А (это из условия, что их скалярное произведение равно нулю): 12х - 5у + С = 0.
Для определения слагаемого С подставим координаты точки С:
12*8 - 5*1 + С = 0, отсюда С = -96 + 5 = -91.
Получаем уравнение общего вида:
СD = 12х - 5у - 91 = 0.
т.к треугольник равнобедренный, то высота это и медиана и биссектриса. следовательно получим два равных прямоугольных треугольника. углы в них 90 30 и 60 градусов
(углы при основании большого треугольника равны так как это равнобедренный треугольник и равны соответственно 180 - 120=60\2=30)
свойство прямоугольных треугольников, что катет лежащий против угла в 30 градусов равен половине гипотенузы
следовательно гипотенуза равна 23*2=46 см
по теореме пифагора находим основание маленького треугольника это 46^=23^2 +x^2
х= 23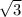
основание большого треугольника 23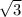
*2 = 46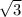
Объяснение: