60°
Объяснение:
рассмотрим полученный ∆АОВ. Он равнобедренный поскольку АО=ВО=радиусу, поэтому прямая СО делит ∆АОВ и угол АОС пополам, поэтому <АОС=<ВОС. В ∆АОВ известны 3 стороны, поэтому мы можем найти угол АОВ, используя теорему косинусов:
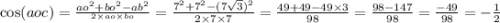
Итак: cosAOB= –1/2=120°.
Так как угол АОС - это половина угла АОВ, то угол АОС=120÷2=60°
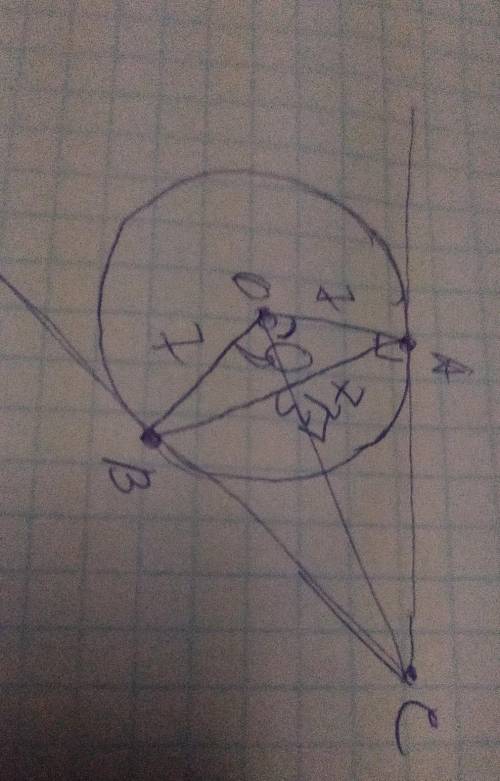
Площадь треугольника можно найти по формуле S=a•h:2 , где а- основание, h- высота, проведенная к нему.
Если у треугольников равны основания и высоты, то их площади равны.
В треугольниках АВК и СВК основания АК=КС, высота из В – общая. Площади этих треугольников равны половине 0,5•SABC.
Следовательно, S ∆ ВСК=0,5 S ∆ АВС.
Рассмотрим ∆ КВС. Точка О делит ВК отношении ВО:ОК=2:1.
Это свойство точки пересечения медианы в задачах встречается нередко.
Высота для ∆ ВОС и КОС общая, поэтому площадь ∆ ВОС равна 2/3 площади ∆ КВС.
А т.к. S ∆ КВС=0,5 S ABC, то S ∆ ВОС=1/3 площади ∆ АВС.⇒
S ∆ АВС=3•S ∆ BOC=18 см²
20°
Объяснение:
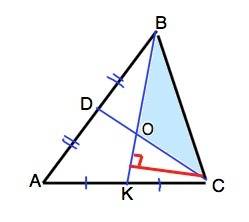
Дано (см. рисунок):
ΔАВС - равнобедренный
AD - биссектриса угла А
BD - биссектриса угла В
∠ADB = 100°
Найти: ∠С
Решение.
Так как треугольник ABC равнобедренный, то у него углы при основании равны ∠А=∠В. Биссектриса делит угол пополам, поэтому α=∠А/2 и β=∠В/2. Но ∠А=∠В и поэтому α=β. Значит, треугольник ADB также равнобедренный.
Найдём углы α и β. Сумма внутренних углов треугольника равна 180°: α + β + 100° = 180°. В силу этого α = β = (180-100)/2 = 40°.
Тогда ∠CАВ=∠СВА=2·α=2·40°=80°. Опять используем свойство:
Сумма внутренних углов треугольника равна 180°.
В силу этого ∠CАВ+∠СВА+∠С=180°. Отсюда
∠C=180°-(∠CАВ+∠СВА)=180°-(80°+80°)=180°-160°=20°.
ответ: 20°
ВC и AС – отрезки касательных, проведённых к окружности с центром в точке О и радиусом 7 см так, что AВ = 7√3 см. Найдите угол АОC. ответ дайте в градусах
Объяснение:
По т. косинусов для ΔОАВ
АВ²=ОА²+ОВ²-2*ОА*ОА cos∠АОВ ,
49*3=2*49-2*49*cos∠АОВ ,
2*49*cos∠АОВ =2*49-3*49
cos∠АОВ =-1*49:(2*49) ,
cos∠АОВ =-1/2 , ∠АОВ=120°.
Т.к. ΔСВО=ΔСАО как прямоугольные( радиус , проведенный в точку касания перпендикулярен касательной) по 2 катетам и общей гипотенузе, то ∠СОВ=∠СОА=120°:2=60°