Здесь даже чертеж не нужен (хотя он для наглядности приложен)
Помним теорему синусов треугольника:
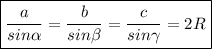
Где угол 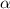 лежит напротив стороны
лежит напротив стороны  , угол
, угол 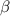 лежит напротив стороны
лежит напротив стороны 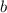 , а угол
, а угол 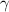 лежит напротив стороны
лежит напротив стороны  , а
, а 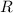 - радиус описанной около треугольника окружности (правда, окружность в этой задаче нам не нужна)
- радиус описанной около треугольника окружности (правда, окружность в этой задаче нам не нужна)
Учитывая, что 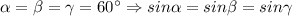
Но тогда теорему синусов можно переписать так:
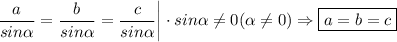
Что и требовалось доказать.
Можно ещё по-другому пойти.
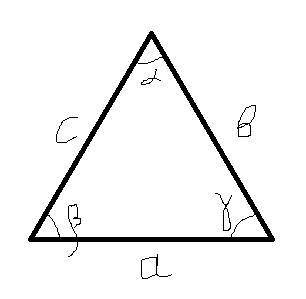
Смотрим на рисунок. 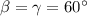 (нижние углы), то есть треугольник равнобедренный с основанием
(нижние углы), то есть треугольник равнобедренный с основанием  , значит, боковые стороны равны, то есть
, значит, боковые стороны равны, то есть 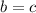
Далее, 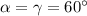 , то треугольник равнобедренный с основанием
, то треугольник равнобедренный с основанием 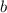 , боковые стороны равны, то есть
, боковые стороны равны, то есть 
Ну и завершающий вывод:
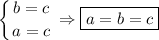
Что и требовалось доказать.
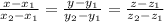
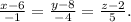
x-6 y-8 z-2
-1 -4 5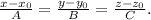
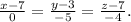
Необходимая для решения точка А3(2; 4; 7) задана по условию, а направляющий вектор для искомой прямой возьмём тот же, что для прямой А1А2, так как они параллельны: n=(-1;-4;5).
ответ: 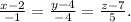
Найдем скалярное произведение векторов а и в
-6*8+(-4)*(-12)=-48+48=0
Вывод. Раз скалярное произведение равно нулю. то векторы перпендикулярны.