
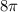 см.
см.
Объяснение:
Радиус окружности, описанной около правильного треугольника со стороной а определяется по формуле :
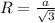
А радиус окружности вписанной в правильный треугольник со стороной а можно найти по формуле :
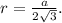
Значит радиус вписанной в правильный треугольник окружности в 2 раза меньше радиуса описанной окружности . Так как по условию
R=8 см, то r =8:2=4 см.
Найдем длину окружности по формуле 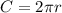 , где r -радиус окружности, вписанной в правильный треугольник, т.е. r =4 см.
, где r -радиус окружности, вписанной в правильный треугольник, т.е. r =4 см.
 см.
см.
Если 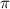 считать приближенно равным 3,14, то
считать приближенно равным 3,14, то
С≈ 8*3,14=25,12 см.
Объяснение:
Отберем корни уравнения, принадлежащие отрезку![[0;\frac{\pi}{4} ]](/tpl/images/1358/5689/59225.png) :
:
так как n-целое число, то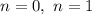
если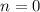 , то
, то 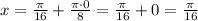
если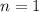 , то
, то 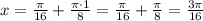
2.
так как n-целое число, то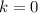
если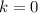 , то
, то 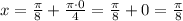
=========================