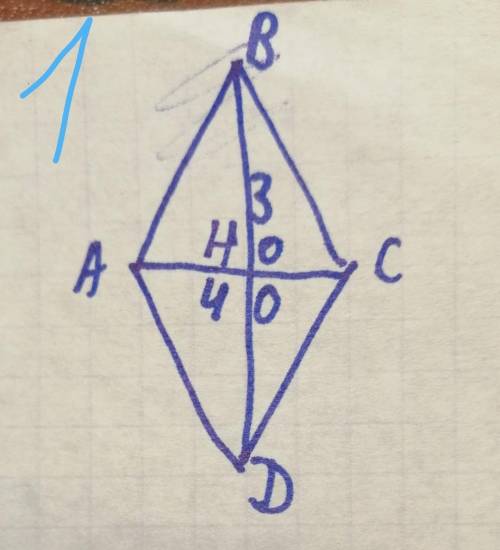
1). АС перпендикулярен ВD т.к. АВСD - ромб (Н - точка пересечения диагоналей)
ВН = НD = 30÷2 = 15
АН = НС = 40÷2 = 20
треуг. АНВ - прямоуг.
По т. Пифагора
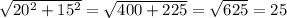
P = 25 * 4 = 100
ответ: 100
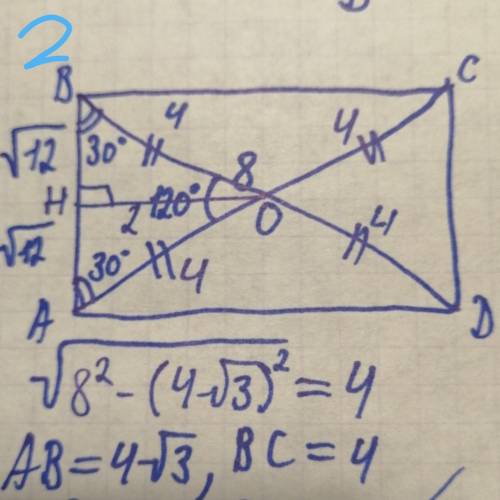
2). Проведем ОН перпендикулярно АВ
АО = ОС = ОВ = ОD (диагонали прямоугольника точкой пересечения делятся пополам)
угол ВОН = углу НОА = 60°
треуг. ВНО - прямоуг., угол НВО = 30° => ОН = 1/2 ОВ = 2
По т. Пифагора
НВ=
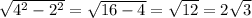
АВ = 2НВ = 4 корня из 3
треуг. АВD - прямоуг
По т. Пифагора
АD =
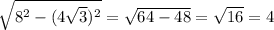
ответ: 2 стороны по 4 корня из 3, 2 стороны по 4
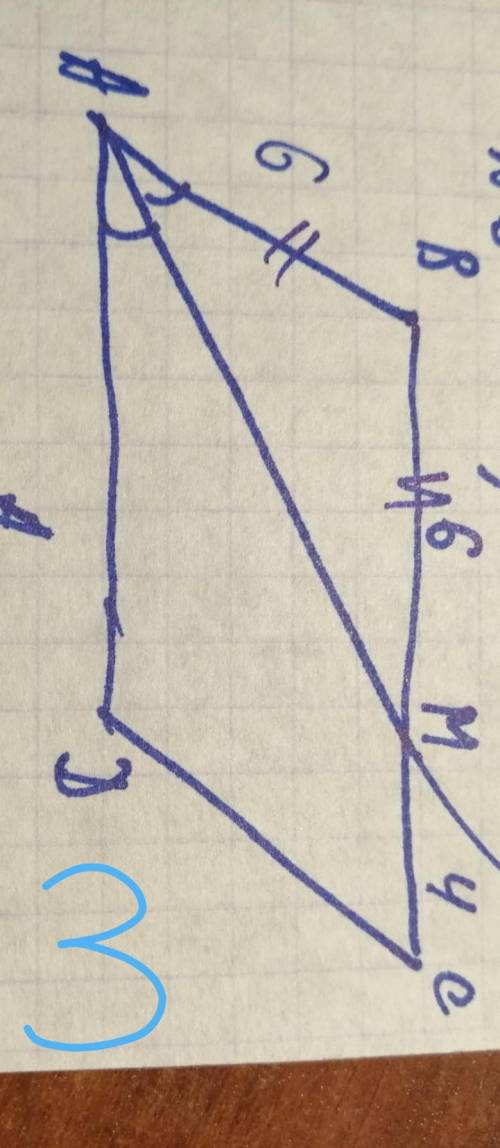
3). Биссектриса параллелограмма отсекает от него р/б треуг. => ВМ = АВ = 6
ВС = ВМ + МС = 6 + 4 = 10
Р = 6 + 6 + 10 + 10 = 32
ответ: 32
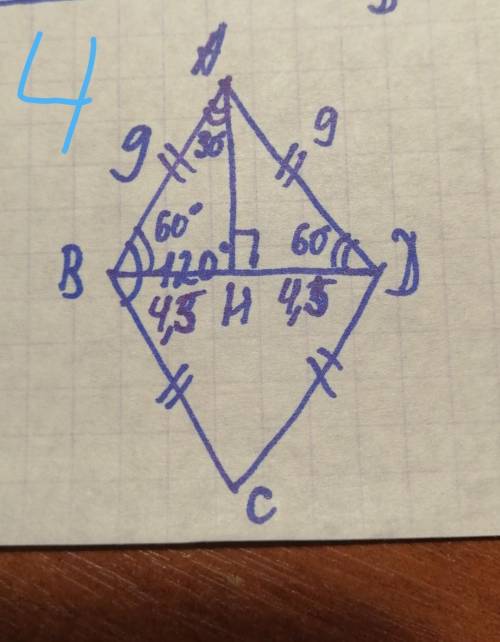
4). АВ = АD = 36÷4 = 9
Проведем АН перпендикулярно ВD
треуг. АВD - р/б, угол АВD = 120°÷2 = 60°
треуг. АВН - прямоуг., угол ВАН = 90° - 60° = 30° => ВН = 1/2 АВ = 4,5 (катет, лежащий против угла в 30°, равны половине гипотенузы)
ВD = 2ВН = 9
ответ: 9
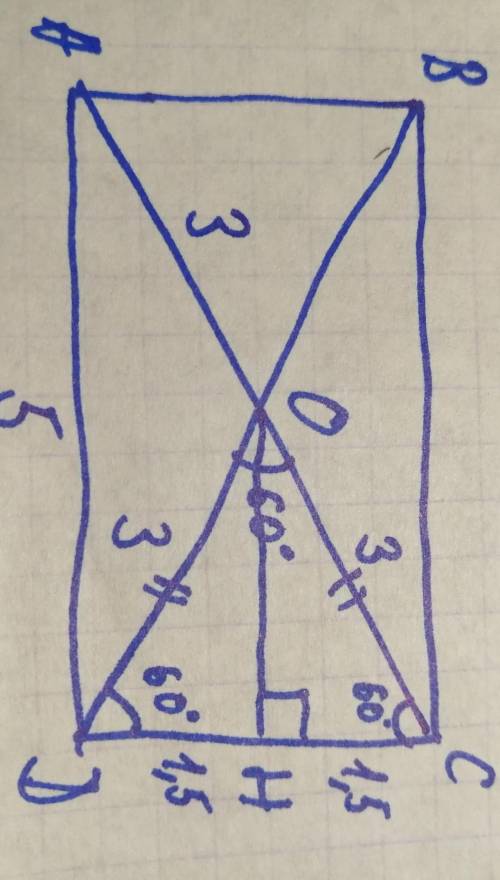
5). Проведем ОН перпендикулярно СD
угол СОН = углу HOD = 60°÷2 = 30°
треуг. СОН - прямоуг., угол СОН = 30° => СН = 1/2 ОС = 1,5 (катет, лежащий против угла в 30°, равны половине гипотенузы) => CD = 3
треуг. АСD - прямоуг.
По т. Пифагора
АD=
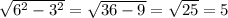
S = 3 * 5 = 15
ответ: 15
1). АС перпендикулярен ВD т.к. АВСD - ромб (Н - точка пересечения диагоналей)
ВН = НD = 30÷2 = 15
АН = НС = 40÷2 = 20
треуг. АНВ - прямоуг.
По т. Пифагора
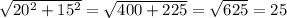
P = 25 * 4 = 100
ответ: 100
2). Проведем ОН перпендикулярно АВ
АО = ОС = ОВ = ОD (диагонали прямоугольника точкой пересечения делятся пополам)
угол ВОН = углу НОА = 60°
треуг. ВНО - прямоуг., угол НВО = 30° => ОН = 1/2 ОВ = 2
По т. Пифагора
НВ=
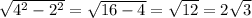
АВ = 2НВ = 4 корня из 3
треуг. АВD - прямоуг
По т. Пифагора
АD =
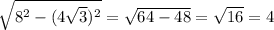
ответ: 2 стороны по 4 корня из 3, 2 стороны по 4
3). Биссектриса параллелограмма отсекает от него р/б треуг. => ВМ = АВ = 6
ВС = ВМ + МС = 6 + 4 = 10
Р = 6 + 6 + 10 + 10 = 32
ответ: 32
4). АВ = АD = 36÷4 = 9
Проведем АН перпендикулярно ВD
треуг. АВD - р/б, угол АВD = 120°÷2 = 60°
треуг. АВН - прямоуг., угол ВАН = 90° - 60° = 30° => ВН = 1/2 АВ = 4,5 (катет, лежащий против угла в 30°, равны половине гипотенузы)
ВD = 2ВН = 9
ответ: 9
5). Проведем ОН перпендикулярно СD
угол СОН = углу HOD = 60°÷2 = 30°
треуг. СОН - прямоуг., угол СОН = 30° => СН = 1/2 ОС = 1,5 (катет, лежащий против угла в 30°, равны половине гипотенузы) => CD = 3
треуг. АСD - прямоуг.
По т. Пифагора
АD=
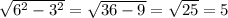
S = 3 * 5 = 15
ответ: 15





3 21/128 или прибл.=3.16
Объяснение:
Проведем биссетрису АР , Р точка пересечения биссектрисы со стороной ВС.
Пользуясь теоремой о биссектрисе (1)
АВ/AC=BP/PC
Найдем ВР и РС
ВР=21:24*9=21*3:8
РС=21:24*15=21*5:8
Тогда длина биссектрисы находится по формуле:
АР²=АВ*АС-ВР*РС=9*15-21*3*21*5:8:8
АР²=2025:64
АР=45/8
Теперь проведем биссектрису ВК. Точка пересечения ее с биссектрисой АР по условию задачи - I.
Pассмотрим треугольник ВАР. По уже упомянутой ранее теореме о биссектрисе (1) AI/IP=AB/BP
AI/IP=9/(21*3/9)=9*9/21/3=9/7 => AI/AP=9/16
Тогда AI= AP:16*9= 45*9/16/8 =3 21/128 или прибл.=3.16