Question

Найдите площадь треугольника, вершины которого имеют координаты A(10; 10), B(4; 10), C(30; 40)

Answer 1

$A(10;10)\ ,\ \ B(4;10)\ ,\ \ C(30;40)\\\\AB=\sqrt{(4-10)^2+(10-10)^2}=6\\\\CH\perp AB\ ,\ \ H(30;10)\ \,\ \ CH=\sqrt{(30-30)^2+(40-10)^2}=30\\\\S_{ABC}=\dfrac{1}{2}\cdot AB\cdot CH=\dfrac{1}{2}\cdot 6\cdot 30=90$

Answer 2

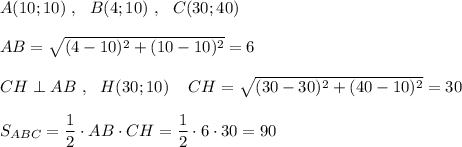
90

Объяснение:

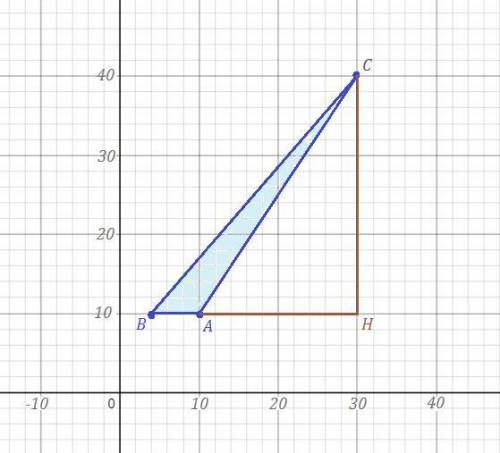
Площадь треугольника = 1/2 АB * CH, где CH - высота

так как у А и В одинаковая координата по оси y, то длина = разности координат по оси х, то есть = 10-4=6 Высота тогда равна разности координаты y точки С и точек A и B = 40-10=30. Тогда площадь = 30*6/2=90