Объем цилиндра равен πR²h=πR²*3=24π⇒R²=8⇒R=√8=2√2
Т.к. образующие конуса пересекают образующие цилиндра, деля их пополам, то в прямоугольном треугольнике, образованном высотой конуса, образующей конуса и радиусом конуса, по теореме Фалеса получаем отношение радиуса конуса к отрезку, равному разности между радиусом конуса и цилиндра, равно двум, значит, радиус конуса больше радиуса цилиндра в два раза. тогда радиус конуса равен 2*2√2=4√2, высота у конуса и цилиндра одна и та же. поэтому объем конуса равен
v=(1/3)*πr²h, где r=4√2, h= 3, v=(1/3)*π(4√2)²*3=32π.
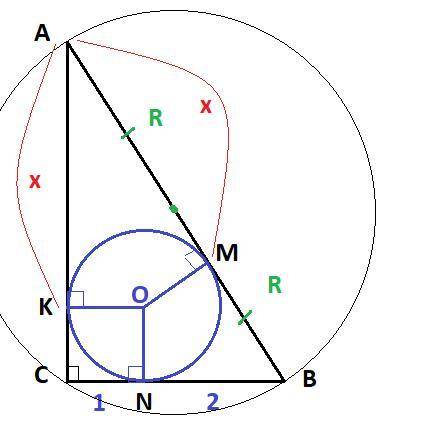
Дано : ΔABC, ∠C = 90°, CN = 1 см, NB = 2 см,
вписанная окружность (O; r)
Найти : S, r, R
Так как окружность вписана в треугольник, то стороны треугольника являются касательными к окружности. Радиус, проведённый в точку касания, перпендикулярен касательной в этой точке.
ON⊥CB, OK⊥AC, OM⊥AB
⇒ CKON - квадрат со стороной, равной радиусу вписанной окружности
⇒ r = CK = KO = JN = CN = 1 см
Отрезки касательных к окружности, проведённые из одной точки, равны
BM = BN = 2 см; AK = AM = x см
ΔABC :
BC = CN + BN = 1 см + 2 см = 3 см
AC = AK + KC = (x + 1) см
AB = AM + MB = (x + 2) см
Площадь прямоугольного треугольника можно вычислить через полупроизведение катетов или через произведение полупериметра на радиус вписанной окружности.
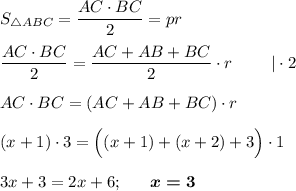
AC = x + 1 = 4 см; AB = x + 2 = 5 см
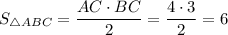 см²
см²
Радиус описанной около прямоугольного треугольника окружности равен половине гипотенузы
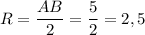 см
см
ответ : S = 6 см², r = 1 см, R = 2,5 см
ответ: а) 150* и 30*; б) 55* и 125*
Объяснение:
В нашем случае образуется 8 углов из которых одна половина равны между собой и вторая половина также равны между собой.
Так ∠1=∠4=∠5=∠8, как накрест лежащие и равны 150*.
А ∠2=∠3=∠6=∠7.
Сумма углов 1 и 2 равен 180*, т.е. получается развернутый угол, а углы смежные. Отсюда найдем ∠2=180*-150*=30*.
б) один из углов на 70* больше другого. обозначим один из углов через х, тогда другой, смежный ему, равен х+70. В сумме они дают 180*.Составим уравнение и найдем х:
х+х+70=180*;
2х+70=180*;
2х=180-70;
2х=110;
х=55* - один из углов (меньший).
55*+70*=125* - больший угол.
Итак, одна половина углов равна 55*, а другая - 125* (смотри предыдущее задание).
Как-то так... :)) Удачи!
ответ: 32π (ед. объема)
Объяснение:
Формула объема цилиндра (R — радиус основания, H — высота):
V=πR²H;
Формула объема конуса (R — радиус основания, Н — высота конуса):
V =πR²Н/3.
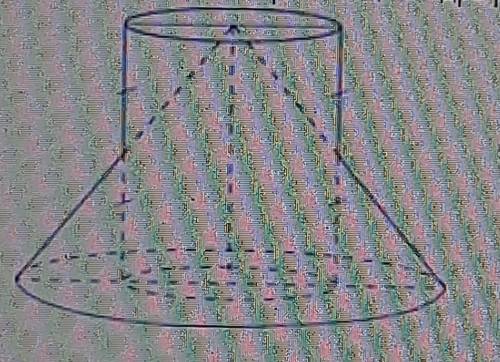
Образующие конуса пересекают образующие цилиндра и делят их пополам ⇒ плоскость, которая проходит через середины образующих цилиндра, параллельна его основанию, поэтому делит пополам и высоту цилиндра, а, следовательно, и его объем.
На рисунке к задаче А₁О₁ - радиус основания половины цилиндра.и равен АО - радиусу основания полного цилиндра, Объем половины цилиндра
V₁=πR²H/2=24π:2=12π;
Радиус и высота конуса А₁СВ₁, вписанного в верхнюю половину цилиндра, равны радиусу и высоте половины цилиндра. ⇒
Объем этого конуса равен π•R²•0,5Н/3.=12π:3=4π (ед. объема)
Высота большого конуса вдвое больше высоты малого, их основания параллельны, образующие большего -продолжение меньшего, следовательно, малый конус и большой - подобны c k=CO:CО₁=2.
Отношение объемов подобных фигур равно кубу их коэффициента подобия.
V(KCM):V(A₁BC₁)=k³
V(KCM)=V(A₁BC₁)•2³=4π•8=32π (ед. объема)
-------------
Вариант решения.
Осевое сечение данного конуса –равнобедренный треугольник КСМ, в котором высота СО⊥КМ и делится средней линией цилиндра А₁В₁ пополам.
Средняя линия прямоугольного треугольника КСО – А₁О₁=R , => КО=2А₁О₁=2R.
V(конуса КСМ)=π•(2R)²•H/3
V(конуса):V(цилиндра)=[π•(2R)²•H/3]:πR²H=4/3 =>
V(конуса)=24π•4/3=32π