Для прямоугольного треугольника справедлива теорема Пифагора : квадрат гипотенузы равен сумме квадратов катетов.
Треугольник с заданными сторонами является прямоугольным.
25² = 7² + 24²
625 = 49 + 576 = 625
Пусть коэффициент пропорциональности равен k, тогда пропорциональные стороны треугольника будут 7k, 24k, 25k
(25k)² = (7k)² + (24k)²
625k² = 49k² + 576k² ⇒ 625k² = 625k²
Для треугольника со сторонами 7k, 24k, 25k тоже справедлива теорема Пифагора, значит, треугольник является прямоугольным.
Пусть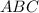
— равнобедренный треугольник, 
; 
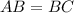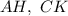— его высоты. У равнобедренного треугольника углы при основании равны, т.е. 
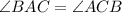. Рассмотрим прямоугольные треугольники 
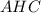и 
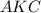. У них сторона 
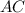общая и 
, следовательно,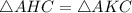 
по гипотенузе и острому углу. Из равенства треугольников следует равенство соответствующих сторон, то есть, 