Объяснение:см. во вложении

1)
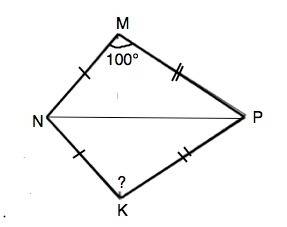
Проведем диагональ NP. Треугольники PMN и PKN равны по трем сторонам - две по условию, третья - общая. .
Следовательно, углы при вершинах К и М равны. Угол К=100°
2)
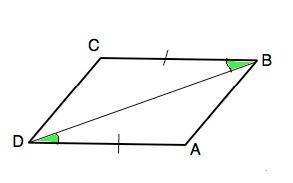
Диагональ BD делит четырехугольник на треугольники ∆ ABD и ∆ CBD. В этих треугольниках стороны ВС=АD по условию, DB общая, углы между этими сторонами равны. ∆ ABD и ∆ CBD равны по первому признаку равенства треугольников.
Следовательно, стороны АВ=CD.
Если противоположные стороны четырехугольника равны, этот четырехугольник - параллелограмм. ⇒, АВ||CD. Доказано.
121°
Объяснение:
1-ый
CH - биссектриса => .
.
Тогда
Задача решена!
2-ой
Внешний угол треугольника равен сумме двух углов треугольника, которые не смежны с ним.
Поэтому верно:
Т.к. треугольник равнобедренный, то .
.
Тогда:
Тогда .
.
Значит
Задача решена!