В треугольнике mkp угол m равен 80 градусам,а угол k-34 градусам.Окружность с центром в точке p пересекает отрезок mp в точке a и отрезок kp-в точке b. Найдите угол bap.Очень желательно чтобы ответ был с чертежом.
В треугольнике mkp угол m равен 80 градусам,а угол k-34 градусам.Окружность с центром в точке p пересекает отрезок mp в точке a и отрезок kp-в точке b. Найдите угол bap
Объяснение:
1)По т. о сумме углов треугольника ∠Р=180°-80°-34°=66°.
2)РА=РВ как радиусы окружности с центром в точке Р⇒ ΔАВр-равнобедренный ⇒∠ВАР=∠АВР= =57°.
Нам дана окружность, значит известен ее центр. 1. Проведем прямую через центр О окружности и данную точку М на окружности. 2. Из точки М на прямой ОМ восстановим перпендикуляр к прямой ОМ. Для этого из точки М как из центра проводим дугу радиусом ОМ и в точке пересечения прямой и этой дуги ставим точку N. Из точек О и N радиусом ОN проводим две дуги и точки их пересечения обозначим А и В. Соединим точки пересечения прямой АВ, которая пройдет через точку М, так как ОМ=MN. эта прямая и есть искомая касательная к окружности в точке М, так как <OMA=<OMB=90° по построению, а касательная перпендикулярна радиусу в точке касания.
Нам дана окружность, значит известен ее центр. 1. Проведем прямую через центр О окружности и данную точку М на окружности. 2. Из точки М на прямой ОМ восстановим перпендикуляр к прямой ОМ. Для этого из точки М как из центра проводим дугу радиусом ОМ и в точке пересечения прямой и этой дуги ставим точку N. Из точек О и N радиусом ОN проводим две дуги и точки их пересечения обозначим А и В. Соединим точки пересечения прямой АВ, которая пройдет через точку М, так как ОМ=MN. эта прямая и есть искомая касательная к окружности в точке М, так как <OMA=<OMB=90° по построению, а касательная перпендикулярна радиусу в точке касания.
В треугольнике mkp угол m равен 80 градусам,а угол k-34 градусам.Окружность с центром в точке p пересекает отрезок mp в точке a и отрезок kp-в точке b. Найдите угол bap
Объяснение:
1)По т. о сумме углов треугольника ∠Р=180°-80°-34°=66°.
2)РА=РВ как радиусы окружности с центром в точке Р⇒ ΔАВр-равнобедренный ⇒∠ВАР=∠АВР=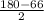 =57°.
=57°.
∠ВАР=57° .