Question

hELp Найти скалярное произведение векторов AK̅̅̅̅ и BL̅̅̅̅, если AK и BL − медианы равнобедренного треугольника ABC, площадь которого равна S, а угол ∠ А = 120°.

Answer 1

Найти скалярное произведение векторов AK̅̅̅̅ и BL̅̅̅̅, если AK и BL − медианы равнобедренного треугольника ABC, площадь которого равна S, а угол ∠ А = 120°.

Объяснение:

1) ΔАВС-равнобедренный , ∠А =120°, АС=АВ=х ,∠В=∠С=(180°-120°):2=30°  . Площадь треугольника равна половине произведения двух сторон на синус угла между ними. По условию она S.

S=1/2*х*х*sin120 ⇒  х²= 2S: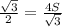 $\frac{\sqrt{3} }{2} =\frac{4S}{\sqrt{3} }$ . х= $\sqrt{\frac{4S}{\sqrt{3} } }$ .

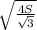По т. синусов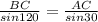   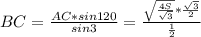$\frac{BC}{sin120} =\frac{AC}{sin30}$   ,  $BC=\frac{AC*sin120}{sin3} =\frac{\sqrt{\frac{4S}{\sqrt{3} } }*\frac{\sqrt{3} }{2} }{\frac{1}{2} }$  , BC=$\sqrt{S*\sqrt{3} }$ .

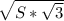2) Используя правила сложения векторов :

вектор АК=0,5(АВ+АС), вектор ВL=0,5(ВА+ВС).   Тогда

Векторы АК*ВL=0,25(АВ*ВА +АВ*ВС +АС*ВА +АС*ВС) .

Посчитаем каждое скалярное произведение

Вектора АВ*ВА=|АВ|*|ВА|*cos180=(4S/√3)*(-1)=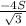$\frac{-4S}{\sqrt{3} }$

Вектора АВ*ВC=|АВ|*|ВC|*cos150=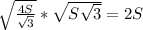$\sqrt{\frac{4S}{\sqrt{3} } }*\sqrt{S\sqrt{3} }=2S$

Вектора АС*ВА=|АС|*|ВА|*cos60=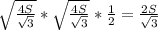$\sqrt{\frac{4S}{\sqrt{3} } }*\sqrt{\frac{4S}{\sqrt{3} } }*\frac{1}{2} =\frac{2S}{\sqrt{3} }$

Вектора АC*ВС=|АC|*|ВС|*cos30=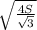 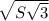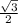$\sqrt{\frac{4S}{\sqrt{3} }}$ *$\sqrt{S\sqrt{3} }$ *$\frac{\sqrt{3} }{2}$ =S√3 .

Для определения угла между векторами, вектора переносились для совмещения начал векторов.Использовались свойства углов параллелограмма, смежных углов ( см. чертеж)

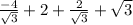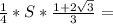
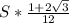АК*ВL=0,25*S( $\frac{-4}{\sqrt{3} }+2+\frac{2}{\sqrt{3} } +\sqrt{3}$ ) =$\frac{1}{4} *S*\frac{1+2\sqrt{3} }{3} =$$S*\frac{1+2\sqrt{3} }{12}$ .