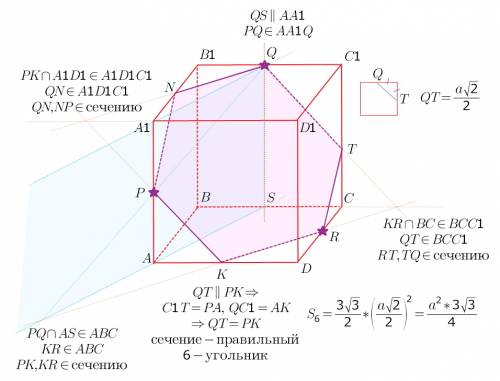
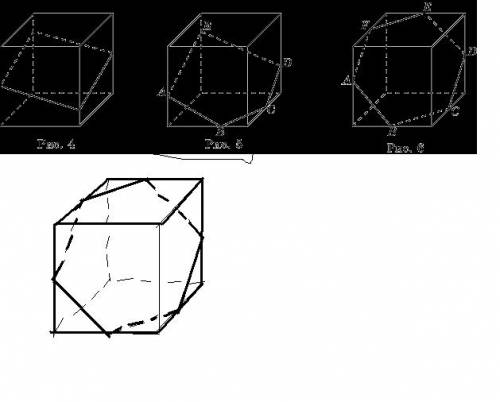
На рисунке 6 показано сечение куба плоскостью в форме шестиугольника ABCDEF. Прямые AB и DE, BC и EF, CD и AF параллельны, как линии пересечения двух параллельных плоскостей третьей плоскостью.
Таким образом, в сечении куба плоскостью может получиться только тот шестиугольник, у которого имеется три пары параллельных сторон.
Так как исходные точки - это середины ребер, то в сечении получается правильный шестиугольник. Обозначим его сторону за "b". b = V((a/2)^2 + (a/2)^2) = (a/2) * V2 = a / V2.
S = 3/2*V3*b^2 = 3/2*V3*(a / V2)^2 = 3V3*a^2 / 4.
1. Верно
2. Не верно
3. Не верно
4. Верно
Объяснение:
Если 2 прямые перпендикулярны к некоторой прямой, то эти прямые параллельные. Поэтому утверждение 1 верно, а 3 нет.
Тупой угол больше 90° и меньше 180° .
Два прямых угла образуют угол 180°, поэтому утверждение 3 не верно.
Развёрнутый угол равен 180°, т.е. его стороны образовывают одну прямую