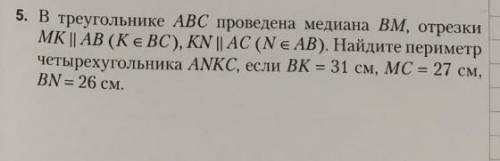
решение. рисунок. данные и ответ во вложении

Объяснение:
а) Пусть СХ=х , тогда ХД=7-х.
Произведение отрезков одной хорды равно произведению отрезков другой хорды ⇒
СХ*ХД=АХ*ХВ,
х*(7-х)=2*6 , 7х-х²=12 ,
х²-7х+12=0, D=49-48=1>0 ,
По т. Виета х₁+ х₂=7
х₁* х₂=12 ⇒ х₁=4, х₂=3 .
Если СХ=4 , тогда ХД=7-4=3.
Если СХ=3 , тогда ХД=7-3=4.
б) ∪ АД=80°, ∪ СВ=48°.∠АХС=180°-∠АХД. Найдем угол ∠АХД по теореме : "Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами " ⇒
∠АХД=(48°+80°):2=64°.
∠АХС=180°-64°=116°.
Объяснение: рисунок к задаче прилагаю.
Дано: ΔABC, т. M ∈ AC (AM = CM), т. K ∈ BC, т. N ∈ AB;
MK || AB, KN || AC, BK = 31 см, MC = 27 см, BN = 26 см.
Найти: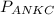 .
.
Решение. Сразу найдем сторону AС. ВМ - медиана ⇒ AС = 2МС = 54 см.
Докажем, что NK - средняя линия треугольника АВС.
Поскольку MK || AB и KN || AC, то четырехугольник AMKN - параллелограмм. А это значит, что NK = AM = 1/2 AC = 27 см ⇒ NK - средняя линия треугольника по определению ⇒ BN = AN = 26 см, BK = KC = 31 см.
Ищем периметр: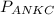 = AN + NK + KC + AC = 26 + 27 + 31 + 54 = 138 см.
= AN + NK + KC + AC = 26 + 27 + 31 + 54 = 138 см.
ОТВЕТ: 138.