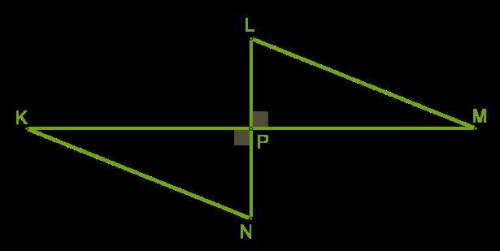
1) 1. Отрезки делятся пополам, значит, KP =РМ, PN = LP, ∡ КPN = ∡ MPL, так как прямые перпендикулярны и оба угла равны 90°. По первому признаку равенства треугольник KPN равен треугольнику MPL.
2. В равных треугольниках соответствующие углы равны. В этих треугольниках соответствующие ∡ К и ∡ M, ∡ N и∡ L. ∡ K = 30°; ∡ N = 60°. ответ. ∡ K = 30°; ∡ N = 60°.
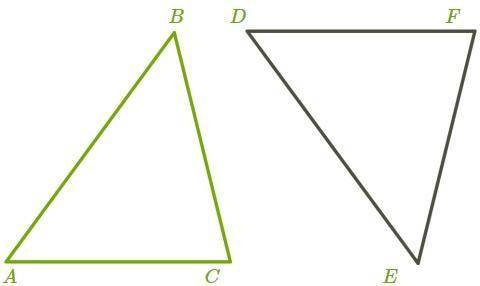
2) 1. Если AB = DE, BC = EF, В = Е, то ΔABC=ΔDEF по первому признаку.
2. AB = DE, BC = EF, CA=FD, то ΔABC=ΔDEF по третьему признаку.
3. AC = DF, ∡ A = ∡ D, С = F, то ΔABC=ΔDEF по второму признаку.
4. AC = DF, ∡ A = ∡ D, AB = DE, то ΔABC=ΔDEF по первому признаку.
5. ∡ B = ∡ E, ∡ C = ∡ F, BC = EF, то ΔABC=ΔDEF по второму признаку.
ответ: время=t=4часа; скорость=v=6км/ч
Объяснение: пусть первоначальная скорость туриста,=х, а время=у. Увеличенная скорость=х+2, а итоговое время =у-1. Зная, что в первом и во втором случае он пройдёт 24км, составиим уравнение:
Первоначально запланировано=ху;
С изменениями=(х+2)(у-1):
(х+2)(у-1)=ху
ху-х+2у-2=ху
ху-ху-х+2у=2
-х+2у=2
х-2у= -2
х=2у-2
Подставим значение х во вторую часть уравнения:
(2у-2)у=24
2у²-2у=24 |÷2
у²-у=12
у²-у-12=0
D=1-4(-12)=1+48=49
y1=(1-7)/2= -6/2= -3
y2=(1+7)/2=8/2=4.
Значение у1 нам не подходит поскольку время не может быть отрицательным, поэтому используем у2 =4. Мы нашли первоначальное время и теперь найдём первоначальную запланированную скорость туриста:
Так как v=s÷t, то:
v=24÷4=6км/ч
Проанализируем каждое утверждение.
1) Сумма смежных углов равна 180°. Если смежные углы равны, то каждый из этих углов равен по 180°:2 = 90°.
ответ: утверждение 1 верно.
2) Если диагонали какого-нибудь четырёхугольника точкой пересечения делятся пополам, то этот четырёхугольник - параллелограмм. Трапеция не является параллелограммом. Следовательно, это неверно.
ответ: утверждение 2 неверно.
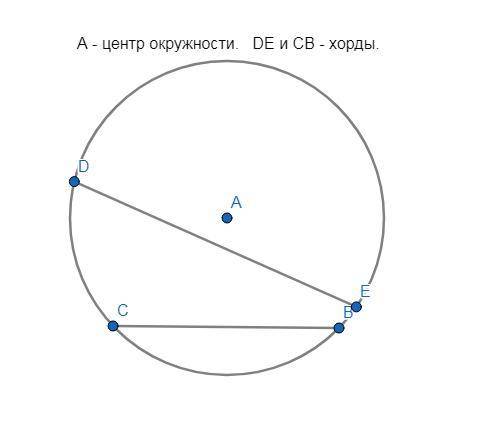
3) Хорда окружности - отрезок, соединяющий любые две точки, лежащих на окружности. Они могут располагаться на разных расстояниях от центра окружности, следовательно, также иметь разную длину.
ответ: утверждение 3 неверно.
ответ: 1.
1. Задание
1.Отрезки делятся пополам, значит КР=РМ
РN=LP
<KPN=<LPN, так как прямые перпендикулярны и оба угла равны 90°.
2.В этих треугольниках соответствующие <К и <М; <N и <L; <K=30°; <N=60°.
2. Задание треугольники.
1 Если АВ=DE,BC=EF; B=E первый признак. (Две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны)
2 АВ=DE; BC=EF; (вот это надо выбрать СA=FD) ( три стороны одного треугольника равны трем сторонам другого треугольника, то эти треугольники равны)
3 АС=DF; <A=<D; <С=<F (два угла и сторона между этими углами одного треугольника равны двум углам и стороне между этими углами другого треугольника, то эти треугольники равны)
4 AC=DF <A=<D; DE=AB (две стороны и угол между ними...)
5 <B=<E; <C=<F; BC=ЕF (два угла и сторона между этими углами)