
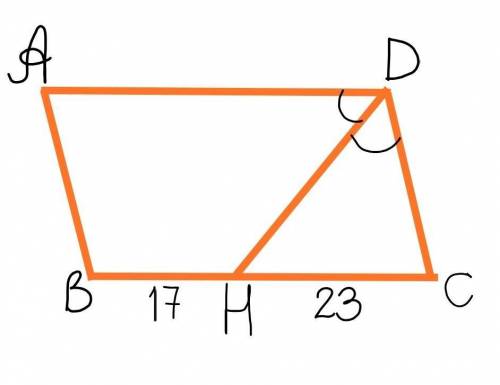
Так как противоположные стороны параллелограмма параллельны, то угол СНD=угол ADH как накрест-лежащие при параллельных прямых AD u BC и секущей DH.
Биссектриса делит угол на два равных угла.
Следовательно угол СDH=угол ADH.
Исходя из найденного: Угол СHD=угол CDH.
Тогда ∆CHD – равнобедренный с основанием HD.
У равнобедренного треугольника боковые стороны равны, тоесть CD=CH=23 см
Противоположные стороны параллелограмма попарно равны.
Следовательно: AD=BC=BH+HC=17+23=40 см; AB=CD=23 см.
Периметр параллелограмма – это сумма длин всех его сторон.
Тоесть Р=AD+AB+BC+CD=40+23+40+23=126 см.
ответ: 126 см.

Объяснение:
1) Рассм. ΔАСВ и ΔABD
CB=BD; ∠CBA=∠ABD; AB - общая
⇒ΔАСВ=ΔABD (1 признак)
3) Рассм. ΔRSO и ΔPOT
RO=OT; PO=OS; ∠ROS=∠POT (вертикалные)
⇒ΔRSO=ΔPOT (1 признак)
5) Рассм. Δ KQM и ΔMFP
QM=MP; ∠KQM=∠FPM; ∠QMK=∠FMP (вертикальные)
⇒Δ KQM =ΔMFP (2 признак)
7)Рассм. ΔEMN и ΔFMN
∠M=∠N; EM=FN; MN-общая
⇒ΔEMN= ΔFMN (1 признак)