За теоремою косинусів ми можемо знайти довжину відрізка AB, використовуючи відомі довжини AO, BO та кут між ними (кут AOB), який дорівнює 120 градусам.
За теоремою косинусів:
AB^2 = AO^2 + BO^2 - 2 * AO * BO * cos(AOB)
Оскільки AO = 3 см, залишається знайти BO та cos(AOB). Для цього розглянемо трикутники АОМ та ВОМ.
У трикутнику АОМ, за теоремою синусів:
BO / sin(30 градусів) = AO / sin(120 градусів - 30 градусів) = AO / sin(90 градусів) = AO / 1
Отже, BO = AO * sin(30 градусів) = 3 см * sin(30 градусів) = 1.5 см.
Аналогічно, у трикутнику ВОМ, за теоремою синусів:
AO / sin(60 градусів) = BO / sin(120 градусів - 60 градусів) = BO / sin(60 градусів)
Отже, AO / BO = sin(60 градусів) / sin(120 градусів - 60 градусів) = sin(60 градусів) / sin(60 градусів) = 1
Отже, BO = AO.
Підставляючи відомі значення в формулу для AB^2, маємо:
AB^2 = (3 см)^2 + (3 см)^2 - 2 * 3 см * 3 см * cos(120 градусів)
AB^2 = 18 см^2
Отже, вiдстань мiж точками A i B дорiвнює квадратному кореню з 18 см^2, тобто:
AB = sqrt(18) см ≈ 4.24 см.
Відповідь від ChatGPT
60√3 см^2
Объяснение:
назвемо трапецію ABCD
S =
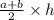
, де S - площа трапеції, a,b - основи, h - висота проведена до основи.
проведемо висоту. назвемо її ВК.
Розглянемо трикутник АВК.
кут К = 90°, отже трикутник прямокутний.
кут А = 60°, за умовою.
за формулою суми кутів трикутника, маємо:
кут В = 180° - 90° - 60° = 30°
за теоремою катета проти кута 30°, маємо:
АК = 12/2 = 6 (см)
знайдемо ВК. за теоремою Піфагора, маємо:
ВК^2 = АВ^2 - АК^2.
ВК^2 = 144 - 36 = 108
ВК = √108 = 6√3
тепер, знайдемо більшу основу.
4+6+6= 16 (см)
підставляємо у формулу:
(4 + 16)/2 × 6√3 = 60√3 (см^2).