1. Берілген нүктелер арқылы өтетін түзудің теңдеуін жазыңыз: А(2;1) В(-1;2). [2 ұпай]
2. Шеңбердің берілген теңдеуі бойынша оның центрінің координаталары мен радиусын табыңыз: (х-4)2 +(у+8)2 =36 [1 ұпай]
3. нүктелері берілген.
a) төбелерінің координаталары бойынша салыңыз; [1 ұпай]
b) қабырғаларының ұзындықтарын табыңыз; [3 ұпай]
c) түрін анықтаңыз (теңқабырғалы, теңбүйірлі, тікбұрышты); [2 ұпай]
d) берілген үшбұрыштың ауданын есептеңіз. [2 ұпай]
4. Төбелері А (1;-1) В (0;1) С (4;3) және Д (5;1) нүктелері болатын төртбұрыштың тіктөртбұрыш болатынын дәлелдеп, оның ауданын табыңыз. Ол үшін:
a) төбелерінің координаталары бойынша сызбасын салыңыз; [1 ұпай]
b) қабырғаларының ұзындықтарын табыңыз; [4 ұпай]
c) диагональдарын анықтап, дәлелдеңіз; [2 ұпай]
d) тіктөртбұрыштың ауданын есептеңіз. [2 ұпай]
комектеесш1. Берілген нүктелер арқылы өтетін түзудің теңдеуін жазыңыз: А(2;1) В(-1;2). [2 ұпай]
2. Шеңбердің берілген теңдеуі бойынша оның центрінің координаталары мен радиусын табыңыз: (х-4)2 +(у+8)2 =36 [1 ұпай]
3. нүктелері берілген.
a) төбелерінің координаталары бойынша салыңыз; [1 ұпай]
b) қабырғаларының ұзындықтарын табыңыз; [3 ұпай]
c) түрін анықтаңыз (теңқабырғалы, теңбүйірлі, тікбұрышты); [2 ұпай]
d) берілген үшбұрыштың ауданын есептеңіз. [2 ұпай]
4. Төбелері А (1;-1) В (0;1) С (4;3) және Д (5;1) нүктелері болатын төртбұрыштың тіктөртбұрыш болатынын дәлелдеп, оның ауданын табыңыз. Ол үшін:
a) төбелерінің координаталары бойынша сызбасын салыңыз; [1 ұпай]
b) қабырғаларының ұзындықтарын табыңыз; [4 ұпай]
c) диагональдарын анықтап, дәлелдеңіз; [2 ұпай]
d) тіктөртбұрыштың ауданын есептеңіз. [2 ұпай]
Объяснение:
ПАМАГИТ
В треугольнике ABC его медианы AA1, BB1 и СС1 пересекаются в точке О. Середины отрезков OA, OB и OC обозначены соответственно A2, B2 и C2. Выразите периметр шестиугольника A2C1B2A1C2B1 через медианы ma = AA1, mb = BB1, mc = CC1.
Объяснение:
Медиана точкой пересечения делится на отрезки в отношении 2:1 ,считая от вершины ( см рисунок 1):
ОА=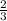 mа , ОВ=
mа , ОВ=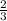 mb , ОС=
mb , ОС=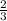 mc .
mc .
Средней линией треугольника называют отрезок, соединяющий середины двух его сторон .Это отрезки :
А₂С₁ и А₁С₂ соответственно в ΔОАВ и ΔОАС ;
С₂В₁ и С₁В₂ соответственно в ΔОСА и ΔОАВ ;
А₂В₁ и А₁В₂ соответственно в ΔОАС и ΔОВС .
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
А₂С₁=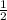 ОВ=
ОВ= 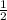 *
*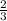 mb =
mb =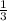 mb , А₁С₂ =
mb , А₁С₂ =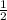 ОВ=
ОВ= 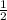 *
*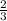 mb =
mb =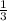 mb ;
mb ;
С₂В₁=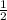 ОА=
ОА= 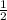 *
*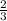 mа =
mа =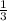 mа , С₁В₂ =
mа , С₁В₂ =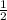 ОА=
ОА= 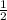 *
*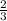 mа =
mа =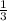 mа ;
mа ;
А₂В₁ =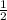 ОС=
ОС= 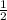 *
*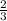 mс =
mс =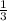 mс , А₁В₂ =
mс , А₁В₂ = 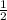 ОС=
ОС= 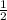 *
*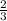 mс =
mс =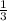 mс .
mс .
Р(шестиугольника)=2*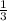 mb+2*
mb+2*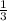 mа+2*
mа+2*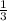 mс=
mс=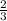 ( mа+ mb+mс)
( mа+ mb+mс)