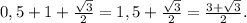проведены три биссектрисы AN, BH и CM. Найдите периметр треугольника ALH.
проведены три биссектрисы AN, BH и CM. Найдите периметр треугольника ALH.
а) ∠ 1 = ∠ 4 = ∠ 5 = ∠ 8 = 20°,
∠ 2 = ∠ 3 = ∠ 6 = ∠ 7 = 160°.
b) ∠ 1 = ∠ 2 = ∠ 3 = ∠ 4 = ∠ 5 = ∠ 6 = ∠ 7 = ∠ 8 = 90°.
с) ∠ 1 = ∠ 4 = ∠ 5 = ∠ 8 = 32°,
∠ 2 = ∠ 3 = ∠ 6 = ∠ 7 = 148°.
Объяснение:
Задание а.
∠ 1 = 20°,
тогда ∠ 2 = 180° - ∠ 1 = 180° - 20° = 160°;
∠ 1 = ∠ 4 = 20° - как углы вертикальные;
∠ 1 = ∠ 5 = 20° - как углы соответственные при параллельных прямых а и b и секущей с;
∠ 5 = ∠ 8 = 20° - как углы вертикальные;
таким образом образом,
∠ 1 = ∠ 4 = ∠ 5 = ∠ 8 = 20°;
аналогично и остальные 4 угла равны между собой:
∠ 2 = ∠ 3 = ∠ 6 = ∠ 7 = 160°.
Задание b.
∠ 1 = ∠ 2 = 180° : 2 = 90°
Согласно доказательству в Задании а):
∠ 1 = ∠ 2 = ∠ 3 = ∠ 4 = ∠ 5 = ∠ 6 = ∠ 7 = ∠ 8 = 90°.
Задание с.
∠ 1 = 32°,
тогда ∠ 2 = 180° - ∠ 1 = 180° - 32° = 148°;
∠ 1 = ∠ 4 = 32° - как углы вертикальные;
∠ 1 = ∠ 5 = 32° - как углы соответственные при параллельных прямых а и b и секущей с;
∠ 5 = ∠ 8 = 32° - как углы вертикальные;
таким образом образом,
∠ 1 = ∠ 4 = ∠ 5 = ∠ 8 = 32°;
аналогично и остальные 4 угла равны между собой:
∠ 2 = ∠ 3 = ∠ 6 = ∠ 7 = 148°.
Если условие такое:
В прямоугольной трапеции АВСД с основаниями 17 см и 25 см диагональ АС является биссектрисой острого угла А. Найдите меньшую боковую сторону трапеции.
То решение такое
Угол а делится биссектрисой на равные углы а и в (а=в)
проведу высоту из вершины А АН=h=СВ
Рассмотрим треугольники
СНА и ВАС
АН=h=СВ
АС - общая
То есть СНА=ВАС => уг.АСН=уг.ВАС=в=а=ДАС => Треуг. СДА -равнобедренный+. АД=СД=17
Рассмотрим треугольник ДНА
ДН=АВ-СД=8
АД=17
По теореме Пифагора АД=корень из(17^2-8^2)= корень из((17-8)*(17+8))=15
CВ=h=АД=15
ответ 15
В равностороннем треугольнике АВС со стороной, равной √3, проведены три биссектрисы : AM, BH, CK. Найдите периметр треугольника ALH.
- - -
Дано :
ΔАВС - правильный (равносторонний).
АВ = √3.
АМ, ВН, СК - биссектрисы.
АМ ∩ ВН ∩ СК = L.
Найти :
Р(ΔALH) = ?
АВ = ВС = АС = √3 (по определению равностороннего треугольника).
В правильном треугольнике все его биссектрисы являются медианами и высотами.Соответственно, по определению медианы треугольника -
АН = НС =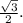
Рассмотрим ΔALH - прямоугольный (так как ∠AHL= 90° по определению высоты).
В равностороннем треугольнике все углы равны по 60°.То есть ∠А = 60°.
По определению биссектрисы треугольника -
∠ВАМ = ∠МАС = 60°/2 = 30°.
По определению косинуса острого угла прямоугольного треугольника -
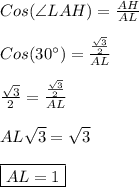
В прямоугольном треугольнике против угла в 30° лежит катет, равный половине гипотенузе.Отсюда -
LH = 0,5*AL = 1*0,5 = 0,5.
Периметр - это сумма длин всех сторон.Отсюда -
Р(ΔALH) = LH + AL + AH =