AB = AC*sin(b)/sin(180-a-b)
где AC - расстояние до некоторой точки С на том-же берегу реки, что и А, b - угол BCA, a - угол BAC - расстояние и углы надо будет измерить
Объяснение:
Очевидно предполагается, что обычной рулеткой и т.п. средствами расстояние AB не измерить из-за воды. Тогда выбираем точку C на одном берегу с A (ну если мы находимся на берегу A) и производим измерения двух доступных нам углов треугольника ABC (примыкающих к вершине A и C) и длину стороны AC. Далее применяем теорему синусов:
AC/sin(b) = AB/sin(с)
где b = 180 - c - a
В треугольнике ABC угол C равен 90°, AB = АС•√2, BC = 6. Найдите высоту CН.
По т.Пифагора АВ²=АС²+ВС²
АВ²-АС²=ВС²
Примем АС=а. Тогда гипотенуза АВ=а√2.
2а²-а²=36⇒
а=√36=6
a√2=6√2
АС=ВС - треугольник равнобедренный. В равнобедренном треугольнике высота, проведенная к основанию, совпадает с медианой.
В равнобедренном прямоугольном треугольнике высота из прямого угла=0,5 гипотенузы ( по свойству медианы из прямого угла).
СН =(6√2):2=3√2
Иногда эту высоту требуется записать в ответе как √2CH. Тогда, так как √2•3•√2=6, в ответе пишется 6.
Объяснение:
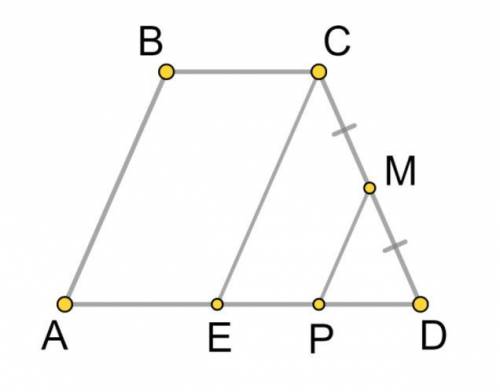
1) АВСД - параллелограмм; АВ=СД=20
ВС=АЕ=12; ЕД=28-12=16;
2)∠ЕДС; СЕ║МР; СМ=МД=20:2=10 (трапеция р/б) ⇒ ЕР=РД=16:2=8 по т. Фалеса.
3) РМ - средняя линия ΔСРД; РМ=СЕ:2=20:2=10.
4) суммируем: РМ=10; ДМ=10; РД=8
Ррмд=10+10+8=28
ответ: 28.