

46.5. Искомая площадь вычисляется:
S=S₁-S₂-S₃,
S₁=π(AB)²/8; S₂=π(AD)²/8; S₃=π(DB)²/8.
S=π/8(AB²-AD²-DB²).
Подставим AB=AD+DB, CD²=AD*DB.
S=π/8(AD²+DB²+2AD*DB-AD²-DB²)=π*AD*DB/4 = π*CD²/4.
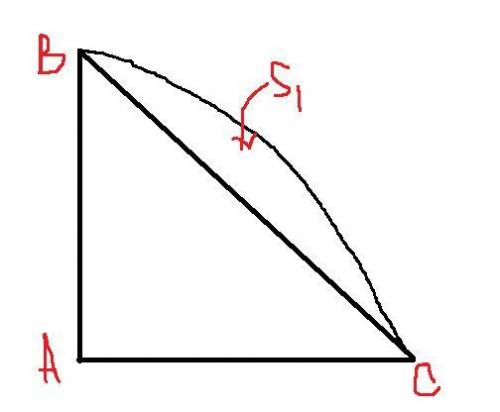
46.4. Рассмотрим четверть квадрата (Рис. ниже) со стороной a. Найдем S₁.
S₁=Sсек -Sтреуг, где Sсек - площадь сектора круга, ограниченного радиусами AB и AC, Sтреуг - площадь треугольника ABC.
Sсек = Sкр/4 = πa²/16.
Sтреуг = a²/8.
S₁ = a²/8*(π/2-1).
Искомая площадь: S=8*S₁ = a²*(π/2-1). По условию a=4 см.
S = 16(π/2-1) см.
46.6. Площадь (из задачи 46.5) вычисляется:
S=π*CD²/4 = π*AD*DB/4 = π*6*4/4 = 6π см².
Длина дуги окружности диаметра AB: L₁=πAB/2=5π см.
Длина дуги окружности диаметра AD: L₂=πAD/2=3π см.
Длина дуги окружности диаметра DB: L=πDB/2=2π см.
Периметр: L=L₁+L₂+L₃ = 5π+3π+2π = 10π см.
Каждый угол шестиугольника равен 120°.
Опустим с вершины С на BD высоту CК, тогда угол BCK=60°, угол CBK=30°.
CK=BC/2, как сторона лежащая против угла 30°. Пусть CK=x, тогда BC=2x.
S=BC*CK*sin(BCK)/2=x*2x*sin(60°)/2=2x^2*sqrt(3)/2=2x^2*sqrt(3)
2x*sqrt(3)=10/2
x^2=10/4*sqrt(3)=10/(4*sqrt(3))
x=sqrt(10/(4*sqrt(3))
то есть сторона шестиугольника равна 2x=2*sqrt(10/4*sqrt(3))
Площадь многоугольника равна:
S=n*a^2/4*tg(360/2n)=(6*10/sqrt(3)):4*tg(30°)=60/sgrt(3) : 4/sqrt(3)=60/4=15