1.
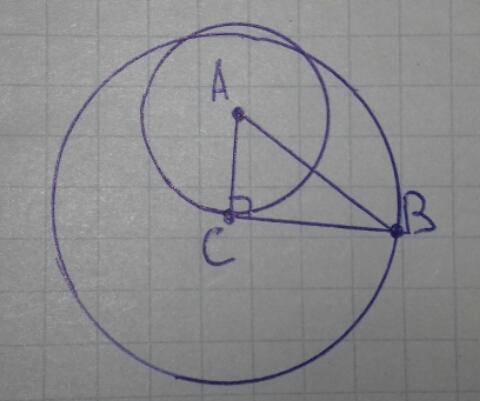
BC⊥AC как катеты прямоугольного треугольника.
BC∩AC = C; AC - радиус окружности с центром A.
Получаем, что BC перпендикулярно радиусу (AC) окружности с центром A и BC пересекает этот радиус в точке (C), принадлежащей той же окружности, поэтому BC это касательная.
2.
AB пересекает окружность (C, CB) в точке B, а CB это радиус той же окружности, проведёный к точке B. Если AB было бы касательной, то AB⊥BC, но это не возможно т.к. AB - гипотенуза, а BC - катет одного прямоугольного ΔABC. Поэтому AB не может быть касательной.
Рассмотрите такой вариант:
1. Углы треугольника, вписанного в окружность, опираются на дуги, которые делят окружность в соотношении 2:3:4 (то есть мера каждой дуги такая: 80°;120°;160°).
2. Из свойств угла, вписанного в окружность, следует, что каждый угол треугольника равен половине дуги, на которую он опирается.
3. Согласно свойству вписанного угла каждый угол треугольника равен соответственно 40°; 60° и 80°.