. 1.Фигуралардың теңдігі. Дене және оның беті 2. Геометрияның негізгі ұғымдары 3. Үшбұрыш дегеніміз не? 4. Төртбұрыш дегеніміз не? 5. Планиметрия қандай бөлім? 6. Стереометрия қандай бөлім?
Сначала докажем, что если окружность описана около прямоугольного треугольника, то ее центр лежит на гипотенузе. пусть, дан треугольник АВС с прямым углом С пусть, точка О-центр описанной окружности. рассмотрим следующие треугольники: ВОС-равнобедренный, ∠ОВС=∠ОСВ, АОС-равнобедренный, ∠ОАС=∠ОСА но сумма углов ВСО и АСО=90°, значит, сумма углов САО + СВО=ВСО +АСО=90° Сумма углов выпуклого четырехугольника =360°,значит, АОВ=360-90-90=180°, то есть развернутый угол Кроме того, ОВ=ОА, поскольку О-центр окружности
задача1 АС = 12 см, ВС = 5 см; АВ=√(СВ²+АС²)=√(144+25)=13 см ОА=ОВ=13:2=7,5 см.
задача2. АС = 16 см, ∠В = 30°. АВ=16:sin30°=16:0,5=32 ОА=ОВ=32:2=16 см
Назовём данный треугольник АВС.
ВВ1- высота к АС.
АА1=СС1 - высоты к равным боковым сторонам.
Высота равнобедренного треугольника, проведенная к основанию, является его биссектрисой и медианой. ⇒
АВ1=СВ1=30:2=15 см
∆ АВВ1=∆ СВВ1 ( по трем сторонам).
Из ∆ АВВ1 по т.Пифагора
ВВ1=√(AB²-AB1²)=√(17²-15²)=8 см
Высоты к боковым сторонам найдем из площади ∆ АВС
Заметим, что ∆ АВС - тупоугольный ( АС² > АВ²+ВС²), поэтому высоты, проведенные к боковым сторонам тупоугольного треугольника, лежат вне его.
S(ABC)=BB1•AC:2=8•15=120 см²
AA1=2S(ABC):BC
AA1=CC1=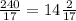 см
см