Объяснение:
При длине рейки в 3 см достичь точки (4,5) невозможно, поскольку расстояние от начала первой рейки до конца второй (в случае, если обе рейки лежат на одной прямой) составляет 3 + 3 = 6 см, а кратчайшее расстояние до точки (4,5) составляет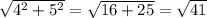 
, что больше 6.
Допустим, нужная нам точка имеет координаты (x,y), а длина рейки равна S. Тогда кратчайшее расстояние до точки равно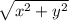 
, и 2 рейки в сочетании с этим расстоянием составляют равнобедренный треугольник со сторонами S, S и .
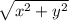По теореме косинусов в треугольнике со сторонами a, b и c и углом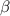 
справедливо соотношение 
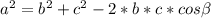. Для нашего треугольника данное выражение примет вид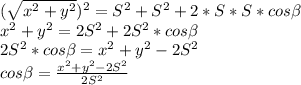 
Отсюда искомый угол будет равен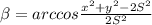 
.
ответ: EF-12 ,FB-6,DE-5
Объяснение: 12+6+5=23+8+6=14+23= 37