дано: δ авс
∠с = 90°
ак - биссектр.
ак = 18 см
км = 9 см
найти: ∠акв
решение.
т.к. расстояние от точки измеряется по перпендикуляру, то опустим его из (·) к на гипотенузу ав и обозначим это расстояние км.
рассмотрим полученный δ акм, т.к. ∠амк = 90°,то ак гипотенуза, а км - катет. поскольку, исходя из условия, катет км = 9/18 = 1/2 ак, то ∠кам = 30°.
т.к. по условию ак - биссектриса, то ∠сак =∠кам = 30°
рассмотрим δакс. по условию ∠аск = 90°; а∠сак = 30°, значит, ∠акс = 180° - 90° - 30° = 60°
искомый ∠акв - смежный с ∠акс, значит, ∠акв = 180° - ∠акс = 180° - 60° = 120°
ответ: 120°
Площадь правильного шестиугольника
S1 =3√3/2 a^2
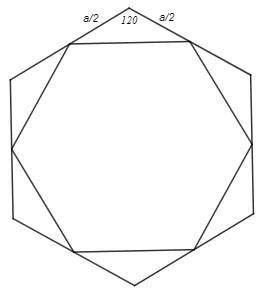
Построим первый внутренний шестиугольник.
Его стороны отсекают 6 равных треугольников, найдем их суммарную площадь.
6 S△ =6 *1/2 (a/2)^2 sin120 =3√3/8 a^2
Видим, что площадь шести треугольников равна 1/4 площади исходного шестиугольника.
Тогда площадь внутреннего шестиугольника равна 3/4 площади исходного.
И так далее.
Имеем бесконечно убывающую геометрическую прогрессию, знаменатель q=3/4.
Первый член b1=3√3/2 (площадь правильного шестиугольника со стороной 1)
Сумма членов бесконечно убывающей геометрической прогрессии
S =b1/(1-q) =3√3/2 : 1/4 =6√3
:11