Найдём сторону a правильного многоугольника, вписанного в окружность с радиусом R:
,
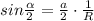где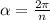 
, n — число сторон правильного многоугольника.
Для правильного треугольника имеем: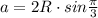 
.
Найдём сторону A правильного многоугольника, описанного около окружности с радиусом r:
.
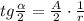Для частного случая правильного треугольника: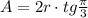 
Окружность у нас одна и та же (R = r).
Находим отношение сторон:
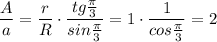
Итак, сторона описанного равностороннего треугольника в два раза больше вписанного.
Площадь равностороннего треугольника со стороной a:
,
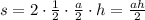где h — высота треугольника,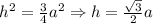 
.
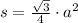
Следовательно, площади относятся друг к другу как квадраты сторон.
P.S. Решения правятся только со второй-третей попытки.
r=в/2√((2а-в)/(2а+в))
Объяснение:
r=√((р-а)(р-в)(р-с))/р
если Δ равнобедренный r=в/2√((2а-в)/(2а+в))