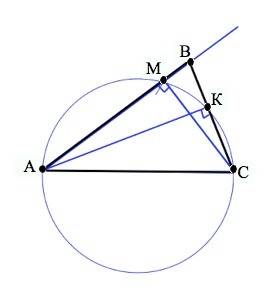
Пусть заданы отрезки: АС - сторона треугольника, АК и СМ - его высоты.. Требуется построить треугольник по данным элементам. • 1) На произвольной прямой откладываем отрезок АС, равный данной стороне. • 2) По известному методу деления отрезка пополам находим середину О отрезка АС и из О радиусом, равным АО, чертится окружность. • 3) Из А на построенной окружности отмечаем циркулем точку К ( длина АК равна длине одной из данных высот). Из точки С таким же образом на окружности отмечаем основание М второй высоты. • 4) Из точки А через М проводим прямую, из точки С через К проводим вторую прямую. Точку пересечения этих прямых обозначим В. Треугольник по стороне АС и высотам АК и СМ построен: Длина АС задана условием. Углы АКС и СМА прямые - опираются на АС как на диаметр окружности. Следовательно, АК - высота к ВС, СМ - высота к АВ.
ответ: 4000/9 см³
Объяснение:
Пирамида правильная, значит в основании лежит квадрат ABCD, высота SO проецируется в точку пересечения диагоналей основания, боковые грани - равные равнобедренные треугольники.
Пусть Н - середина CD. Тогда
SH⊥CD как медиана и высота равнобедренного треугольника SCD,
ОН⊥CD, как медиана и высота равнобедренного треугольника COD (диагонали квадрата равны и точкой пересечения делятся пополам), значит
∠SHO = 60° - линейный угол двугранного угла при основании.
ΔSHO: ∠SOH = 90°,
OH = SO · ctg60° = 10 · √3/3 = 10√3/3 см
ОН - средняя линия ΔACD, значит
AD = 2 · ОН = 20√3/3 см
Sabcd = AD² = (20√3/3)² = 400 · 3 / 9 = 400/3 см²
V = 1/3 · Sabcd · SO = 1/3 · 400/3 · 10 = 4000/9 см³