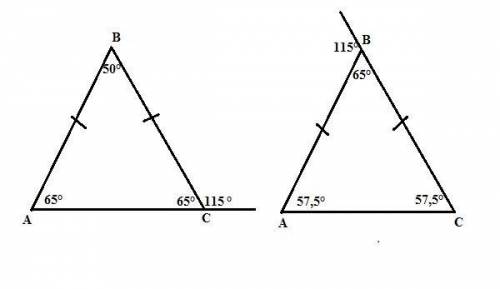
1. 65°, 65°, 50°.
2. 57,5°; 57,5°; 65°.
Объяснение:
Нам дан один из внешних углов равнобедренного треугольника. У равнобедренного треугольника углы при основании равны.
Значит возможны два варианта решения:
1. Если дан внешний угол при основании, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Тогда угол при вершине треугольника равен 180° - 2·65° = 50° (по сумме внутренних углов треугольника, равной 180°).
ответ: 65°, 65°, 50°.
2. Если дан внешний угол при вершине, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Внешний угол треугольника равен сумме двух внутренних (в нашем случае равных), не смежных с ним углов. Следовательно, углы при основании такого треугольника равны 115°:2 = 57,5°.
ответ: 57,5°; 57,5°; 65°.
38
Объяснение:
1) Так как по условию сказано, чо угол ACB=90 градусов, то получается, что треугольник ABC - прямоугольный.2) По условию сказано, что СD-медиана, то есть по особому свойству медианы в прямоугольном треугольнике получаем, что AD=DB=DC (Особое свойство медианы: медиана соединяет одну сторону с серединой другой стороны).3) Треугольники ADC и BDC равнобедренные, так как AD=DB=DC. А в равнобедренном треугольнике: если стороны равны, то и углы равны, то есть в треугольнике BDC: угол B = углу DCB = 52 градуса.4) Угол ACD = угол C - угол DCB;Угол ACD = 90 - 52 =38 градусов.ответ: Угол ACD = 38 градусов.