Объяснение:
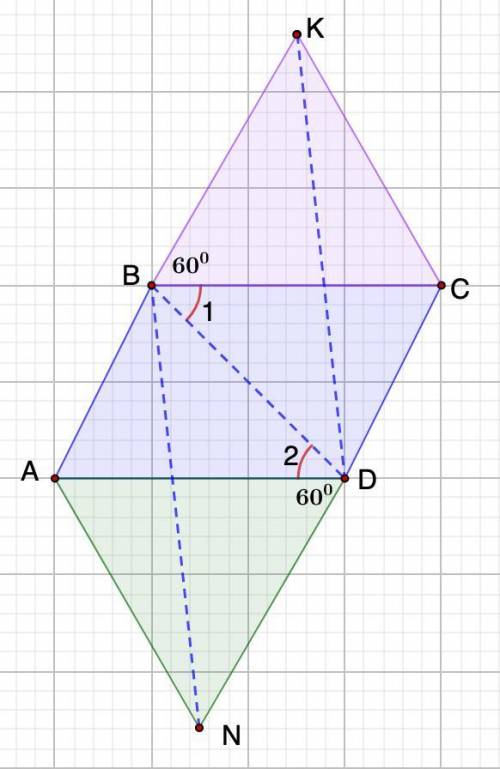
Дано: ABCD - параллелограмм.
ΔВКС и ΔAND - равносторонние.
Доказать: BKDN - параллелограмм.
Доказательство:
1. Рассмотрим ΔВКС и ΔAND - равносторонние.
Противоположные стороны параллелограмма равны.⇒ ВС = AD
⇒ ΔВКС = ΔAND (по трем сторонам, 3 признак)
⇒ BK = ND
2. ВС || AD (ABCD - параллелограмм)
∠1 = ∠2 (накрест лежащие при ВС || AD и секущей BD)
В равностороннем треугольнике углы равны 60°.⇒
∠DBK = ∠1 + 60°
∠BDN = ∠2 + 60°
⇒ ∠DBK + ∠BDN - накрест лежащие при BK и ND и секущей BD.
Если при пересечении двух прямых третьей накрест лежащие углы равны, то прямые параллельны.⇒ BK || ND
Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник - параллелограмм.⇒ BKDN — параллелограмм
2. Рассмотрим треугольник DBE.
Это равнобедренный треугольник, так как по условию BD = BE.
∠BDE = ∠BED, так как это углы при основании равнобедренного треугольника.
3. Определим ∠BDA и ∠BEC.
∠BDA и ∠BDE смежные, поэтому
∠BDA = 180° - ∠BDE.
Аналогично ∠BEC и ∠BED смежные, поэтому
∠BEC = 180° - ∠BED.
Так как ∠BDE = ∠BED, то и ∠BDA = ∠BEC.
4. Рассмотрим треугольники ABD и CBE.
Эти треугольники равны по двум сторонам и углу между ними:
BD = BE и AD = CE - по условию;
∠BDA = ∠BEC.
Следовательно, и стороны BA и BC равны.
Значит, треугольник ABC -равнобедренный.
Знаешь ответ?
Объяснение:
обозначим вершины треугольника А В С с прямым углом С, катетами АС и ВС и гипотенузой АВ. Найдём гипотенузу по теореме Пифагора:
АВ²=АС²+ВС²=2²+3²=4+9=13; АВ=√13
1) тангенс - это отношение противолежащего от угла катета к прилежащему катету, поэтому
tgB=AC/BC=2/3
2) углом лежащим напротив меньшего катета также будет угол В. Синус угла это отношение противолежащего от угла катета к гипотенузе поэтому sinB=AC/AB=2/√13
3) угол прилежащий к большому катету, также является <В. Косинус угла - это отношение прилежащего к углу катета к гипотенузе поэтому
cosB=BC/AB=3/√13
4) в этом случае нам нужно будет найти котангенс угла А, так как он лежит напротив большего катета ВС. Котангенс угла - это отношение прилежащего к углу катета к противолежащему:
ctg=АС/ВС=2/3