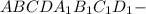 правильная четырехугольная призма
правильная четырехугольная призма
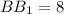 см
см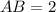 см
см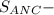 ?
?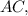 так как
так как 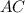 ⊂
⊂ 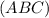 и
и 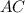 ⊂
⊂ 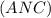
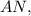 так как
так как 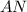 ⊂
⊂ 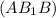 и
и 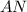 ⊂
⊂ 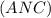
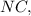 так как
так как  ⊂
⊂ 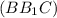 и
и  ⊂
⊂ 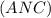
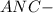 искомое сечение
искомое сечение 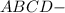 квадрат
квадрат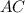 ∩
∩ 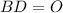
 см
см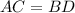 ( как диагонали квадрата)
( как диагонали квадрата)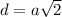
 см
см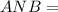 Δ
Δ 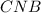 ( по двум катетам) ⇒
( по двум катетам) ⇒ 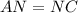
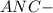 равнобедренный
равнобедренный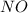 ⊥
⊥ 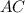
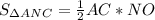
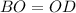
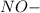 средняя линия Δ
средняя линия Δ 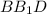
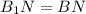 (по условию)
(по условию) 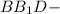 прямоугольный
прямоугольный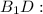
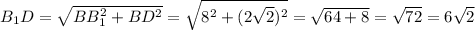 см
см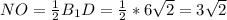 см
см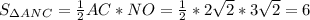 cм²
cм²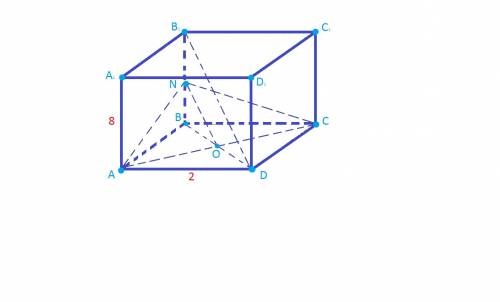
Пусть куб единичный.
Пусть A- начало координат
Ось X- AB
Ось Y - AD
Ось Z - AA1
Вектора
D1C ( 1;0;-1)
B1D (-1;1;-1)
D1C*B1D = 1* (-1) + 0*1 + (-1)*(-1) = 0
Угол 90 градусов
Вектор
AB1(1;0;1)
Плоскость ABC1 - проходит через начало координат .
Уравнение
ax+by+cz=0
Подставляем координаты точек B(1;0;0) и С1(1;1;1)
a=0
a+b+c=0
Пусть b=1 тогда с= -1
Искомое уравнение
y-z=0 Нормаль (0;1;-1)
Синус угла между (AB1 ; ABC1 ) = | (1;0;1)*(0;1;-1) | / | AB1 | / | (0;1;-1) | = 1/2
Угол 30 градусов.