1.
М - середина АВ, значит МВ = АВ/2
Р - середина МВ, значит РВ = МВ/2 = АВ/4
К - середина ВС, значит КС = ВС/2
Е - середина КС, значит ЕС = КС/2 = ВС/4
N - середина АС, значит NA = АС/2
G - середина NA, значит GA = NA/2 = AC/4
По условию
PB + EC + GA = 12
АВ/4 + ВС/4 + АС/4 = 12
1/4 · (АВ + ВС + АС) = 12
АВ + ВС + АС = 12 · 4 = 48 (см)
2.
Из решения первой задачи следует, что
АР = 3/4 АВ
ВЕ = 3/4 ВС
CG = 3/4 AC
По условию
AP + BE + CG = 108
3/4 АВ + 3/4 ВС + 3/4 АС = 108
3/4 · (АВ + ВС + АС) = 108
АВ + ВС + АС = 108 · 4/3 = 144 (см)
площадь трапеции равна 63cos31° +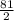
sin62° , что приблизительно равно 89.76
Объяснение:
Достроим рисунок высотами BE и CF.
Отметим, что площадь трапеции ABCD будет совпадать с площадью прямоугольника AFCG = AF*CF = (AE+EF)*BE = (7+AE)*BE
∠ABC=∠CBD=121° , ∠EBC=90° значит ∠ABE=31°
В прямоугольном треугольнике ABE
sin∠ABE=AE/AB ⇒ sin31°=AE/9 ⇒ AE=9*sin31°
cos∠ABE=BE/AB ⇒ cos31°=BE/9 ⇒ BE=9*cos31°
Значит искомая площадь = (7+AE)*BE = (7+9*sin31°)*9*cos31° =
= 63cos31° + 81sin31°cos31° = 63cos31° +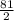
sin62° ≈ 89.76