Обозначим этот треугольник АВС, с вершиной В, основанием АС и высотой ВН. Высота ВН делит ∆АВС на 2 одинаковых прямоугольных треугольников АВН и ВСН, так как треугольник равнобедренный; также ВН является в равнобедренном треугольнике ещё и медианой, поэтому высота ВН делит АС пополам и АН=НС. Рассмотрим один из них, к примеру ∆АВН. Боковая сторона АВ является в нём гипотенузой, а высота ВН - катетом. Найдём по теореме Пифагора катет АН. АН=29²-21²=√(841-441)=√400=20см
АН=НС=20см, тогда АС=20×2=40см
Основание АС=40см.
Теперь найдём площадь ∆АВС по формуле: ½ ×a×h, где h- высота, "а"- сторона, к которой проведена высота:
S= ½ × 40×21=420см²; S=420см²
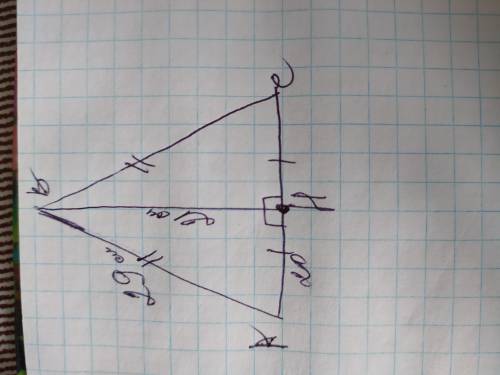
Сделаем рисунок к задаче.
Высота этой трапеции отсекает от нее прямоугольный равнобедренный треугольник с гипотенузой 3√2.
Такой треугольник - половина квадрата с диагональю=гипотенузе.
Формула диагонали квадрата ( формула гипотенузы равнобедренного прямоугольного тр-ка).
d=а√2, где а- сторона квадрата, а в равнобедренном прямоугольном треугольнике - катет. Знание этой формулы часто избавляет от лишних вычислений.
d=СК
СК =3√2=СН√2
СН√2=3√2
СН=3 см
СН=НК как равный катет.
АК=2НК
ВС=АК:2
Площадь трапеции равна Н*(АВ+ВС)
S=3*(3+6):2=13,5 см²
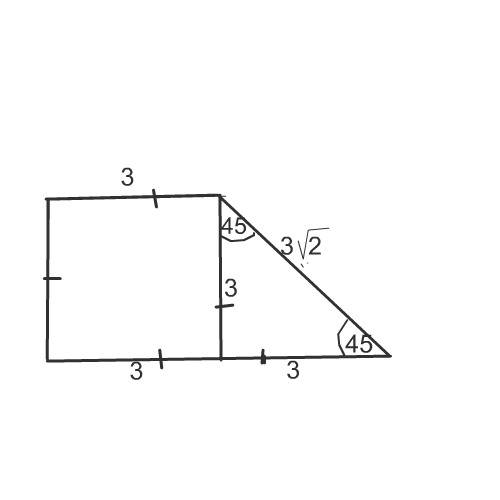
6. RMN - правильный => RN=NM=MR=6
RK - высота, медиана, биссектриса => NK=KM=3
По теореме Пифагора: RM^2=MK^2+RK^2 => RK=/RM^2-RK^2=/36-9=5
ответ:5
7. MPR- прааильный => MP=PR=RM=x
RT - высота, медиана биссектриса =8 =>PT=x:2
По теореме Пифагора: PR^2=PT^2+RT^2
x2=-4 - не подходит по условию
ответ: 4
*Если тебе поставь сердечко:) Тебе не сложно - мне приятно♡
**Правильный треугольник - все стороны равны
*** Теорема пифагора: гипотенуза в квадрате равна катет в квадрате плюс другой катет в квадрате
****число или буква в "^2" - число или буква в квадрате