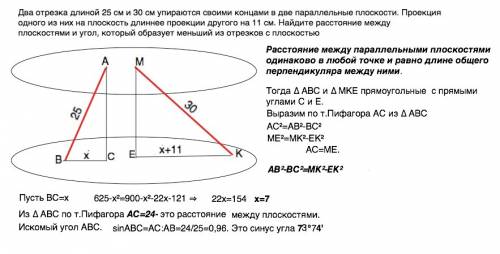
Пусть отрезки будут АВ=25 см с проекцией ВС и МК=30 см с проекцией КЕ.
Расстояние между параллельными плоскостями одинаково в любой точке и равно длине общего перпендикуляра между ними.
Тогда ∆ АВС и ∆ МКЕ прямоугольные с прямыми углами С и Е.
Выразим по т.Пифагора АС из ∆ АВС
АС²=АВ²-ВС²
МЕ²=МК²-ЕК²
АС=МЕ.
АВ²-ВС²=МК²-ЕК²
Пусть ВС=х
625-х²=900-х²-22х-121 ⇒
-900+625+121= х²-х²-22х Проведя необходимые вычисления, получим
22х=154 ⇒ х=7
Из ∆ АВС по т.Пифагора АС=24- это расстояние между плоскостями.
Искомый угол АВС.
sin∠ABC=АС:АВ=24/25=0,96. Это синус угла 73°74'
Видимо, в основании лежит параллелограмм, надо было это написать :)
Диагональ D прямого параллелепипеда в прямоугольном тр-ке, образованном этой диагональю, диагональю основания d и боковым ребром c, является гипотенузой.
Заданы d1 = 12 и с = 5
По теореме Пифагора:
D1^2 = d1^2 + c^2 = 12^2 + 5^2 = 144 + 25 = 169
D1 = sqrt(169) = 13
Найдём вторую диагональ d2 параллелограмма, являющегося основанием параллелепипеда. Cтороны параллелограмма заданы а = 6 и b = 8.
Для этого используем теорему косинусов для обеих диагоналей d1 и d2
d1^2 = a^2 + b^2 - 2ab cos (alfa)
d2^2 = a^2 + b^2 + 2ab cos (alfa)
Если сложить эти уравнения, то получим
d1^2 + d2^2 = 2(a^2 + b^2)
d2^2 = 2(a^2 + b^2) - d1^2
d2^2 = 2(6^2 + 8^2) - 12^2 = 2(36 + 64) - 144 = 2 * 100 -144 = 200 - 144 = 56
Теперь мы можем найти и 2-ю диагональ параллелепипеда D2 так же, как нашли 1-ю, т.е по теореме Пифагора:
D2^2 = d2^2 + c^2 = 56 + 5^2 = 56 + 25 = 81
D2 = sqrt(81) = 9
ответ: Диагонали параллелепипеда равны 13см и 9 см.