
1 по трём сторонам
2 по двум сторонам и углу и
между ними
3 по стороне и двум прилежащим к ней углам
4по стороне и двум прилежащим к ней углам или по двум сторонам и углу между ними
5 по стороне и двум прилежащим к ней углам вроде тоже
6 по трём сторонам
7 по двум сторонам и углу между ними
8 по трём сторонам
9 по стороне и двум прилежащим к ней углам
не точно
ответ:√137 (ед. длины)
Объяснение:
Площадь треугольника равна половине произведения высоты на сторону, к которой проведена. Тогда: Ѕ=а•h:2 ⇒ a•h=2S
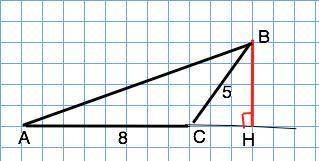
Высота тупоугольного треугольника, проведенная из вершины острого угла, проходит вне треугольника и пересекает продолжение стороны, к которой проведена.
В ∆ АВС проведенная к стороне, равной 8 см, высота ВН=2•16:8=4. Тогда в "египетском" треугольнике ВСН отрезок СН=3 ( то же получим по т.Пифагора).
Треугольник АВН - прямоугольный, АН=8+3=11. По т.Пифагора его третья сторона АВ=√(АН²+BH²)=√(11²+4²)=√137
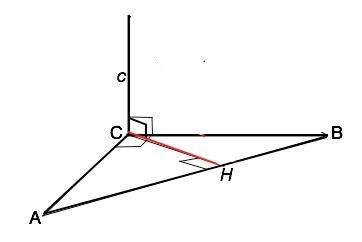
Прямая АВ лежит в плоскости АВС, а прямая с эту плоскость пересекает в точке С, не принадлежащей прямой АВ.
Прямая с и прямая АВ - скрещивающиеся.
Расстояние между скрещивающимися прямыми измеряется длиной их общего перпендикуляра.
Проведем СН⊥АВ.
Прямая с перпендикулярна плоскости АВС, следовательно, перпендикулярна любой прямой в этой плоскости.⇒ с⊥СН
Длина СН - искомое расстояние.
СН⊥АВ и является высотой ∆ АВС.
Из площади прямоугольного треугольника
S=0,5•AC•СB
S=0,5•CH•AB⇒
СН=АС•ВС:АВ
По т.Пифагора АВ= √(AC*+BC*)=√(9+16)=5 дм
СН= 3•4:5=2,4 дм
я хз лол
Объяснение:
спс за