1 признак равенства треуоольников: если 2 стороны треугольника и угол между ними соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны
2 признак: если сторона и прилежащие к ней 2 угла одного треугольника соответственно равны стороне и 2 прилежащим к ней угла другого треугольника, то такие треугольники равны
3 признак: если 3 стороны одного треугольника соответственно равны 3м сторонам другого,то такие треугольники равны
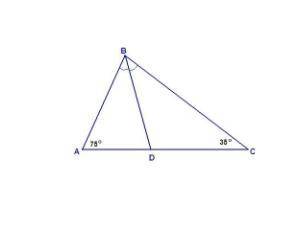
В условии опечатка: надо доказать, что ΔBDC равнобедренный.
ΔBDC равнобедренный,
AD < DC.
Пошаговое объяснение:
а) Зная, что сумма углов треугольника 180°, найдем угол АВС:
∠АВС = 180° - (∠А + ∠С) = 180° - 110° = 70°
Так как BD биссектриса угла АВС, то
∠ABD = ∠CBD = 70°/2 = 35°.
В треугольнике BDC два угла равны, значит он равнобедренный по признаку равнобедренного треугольника.
б) В треугольнике напротив меньшего угла лежит меньшая сторона.
В ΔABD AD < BD, так как AD лежит напротив угла 35°, а BD напротив угла в 75°.
Но BD = DC (доказано выше), тогда
AD < DC
надеюсь , если да то можешь пометить лучшим ответом