В условии задачи ошибка: GH=15 см.
24 см.
Пошаговое объяснение:
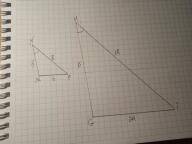
Дано: ΔMNP; МN=5 cм NP=6 см, MP=8 см; Δ GHI; GH=5 см, HI=18 см. ∠N=∠Н. Найти GI.
МN/GH=NP/HI=1/3
Треугольники MNP и GHI подобны по двум сторонам и углу между ними.
Значит МР/GI=1/3; МР=8 см, значит GI=8*3=24 см.
2/3ч=60мин/3*2=40мин-время сближение
24.6км/ч=24.6км/ч/60мин=0.41 км/мин-скорость велосипедиста за 1 мин
Пускай скорость мотоциклиста будет -х км/мин.,
Тогда скорость сближения будет (х-0.41км/мин).
Встретились они через 40 мин, тогда: 40*(х-0.41)=34.5
40х-16.4=34.5
40х=34.5+16.4
40х=50.9
х=50.9/40
х=1.2725км/мин-скорость мотоциклиста за 1 мин
1.2725км/мин*60мин=76.35км/ч-скорость мотоциклиста
Проверка:
1) 76.35-24.6=51.75км/ч-скорость сближение или 51.75км/ч/60мин=0.8625км/мин
2) 0.8625км/мин*40 мин=34.5км
ответ: скорость мотоциклиста 76.35 км/час
Пошаговое объяснение:
найдем угол N
По теореме косинусов в треугольнике MNP:
MP^2=MN^2+NP^2-2*MN*NP*cosN
64=25+36-60cosN
cosN=-1/20=cosH
по теореме косинусов в треугольнике GHI:
GI^2=GH^2+HI^2-2cosH*GH*HI
GI^2=25+324+9
GI^2=358
GI=(корень из 358)