
пересекаются, я к сожалению не могу нарисовать, но могу объяснить. Пересекаются как буква х , а точка пересечения это ее середина. Так вот от этой точки они начинают делиться еще напополам, а доказать равенство треугольников можно по признакам. Есть 2 признака:
1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
2.Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Сказал(а) подсказать, а не решать, так что вот тебе подсказочки)
Объяснение:
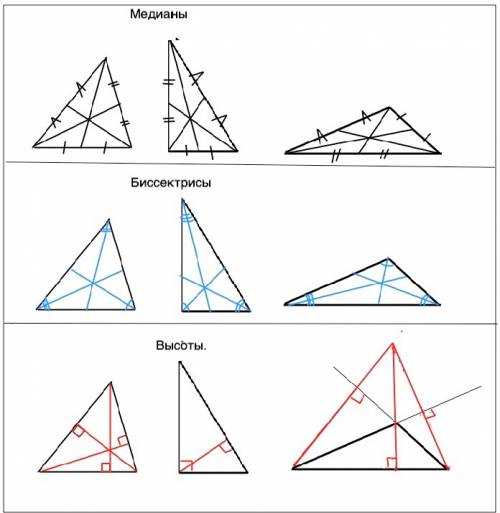
Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины.
Биссектрисы треугольника пересекаются в одной точке, расстояние от которой до сторон треугольника одинаково и является центром вписанной окружности.
Высоты треугольника пересекаются в одной точке. Точка пересечения высот остроугольного треугольника находится внутри него. Точка пересечения высот прямоугольного треугольника - вершина прямого угла.
Высоты тупоугольного треугольника, проведенные из вершин его острых углов, проходят вне его и пересекают продолжения сторон. Точка пересечения высот тупоугольного треугольника находится вне треугольника.
Продлим AO до пересечения с CD в точке F.
BAF=DFA (накрест лежащие при AB||CD)
BAF=DAF (AO - биссектриса BAD)
DAF=DFA => △ADF - равнобедренный, AD=FD
△AOB~△FOE (по двум углам)
AB/FE =OB/OE =4/3 => FE =3/4 AB
DE =1/2 CD =1/2 AB
AD =FD =FE+DE =3/4 AB +1/2 AB =5/4 AB
ответ: AD/AB =5/4