Дано :
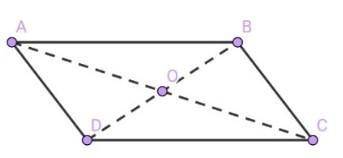
Четырёхугольник ABCD — параллелограмм.
AD = 30.
Отрезки BD и AC — диагонали.
АС = 43.
BD = 35.
Найти :
S(ABCD) = ?
Диагонали параллелограмма, пересекаясь, делятся пополам и образуют четыре равновеликих (равных по площади) треугольника.То есть —
AO = OC = 43 : 2 = 21,5.
DO = OB = 35 : 2 = 17,5.
S(∆AOD) = S(∆AOB) = S(∆BOC) = S(∆DOC).
Рассмотрим ∆AOD.
Найдём его площадь по формуле Герона —
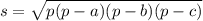
Где s — площадь треугольника; р — полупериметр (одна вторая суммы сторон треугольника) треугольника; а, b и с — длины сторон треугольника.
Найдём р ∆AOD.
p(∆AOD) = 0,5*(AO + DO + AD) = 0,5*(21,5 + 17,5 + 30) = 0,5*69 = 34,5.
Теперь подставляем всё в формулу Герона —
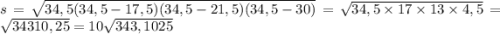
По выше сказанному S(ABCD) =
(10√343,1025) * 4 = 40√343,1025 (ед²).
40√343,1025 (ед²).
KL=27
KN=24
MN=8
Найти: Р(KMN)=?
Решение
Пусть LN=x, а KM=y (рисунок во вложении). KN является биссектрисой в ΔKLM. Используя свойство биссектрисы составим пропорцию: KL/LN=KM/MN.
По условиям задачи KL=27, MN=8, LN=x и KM=y. Подставим значения: 27/х=у/8
Выразим х*у:
х*у=27*8=216 (1)
Найдём длину биссектрисы KN:
KN²=KL*KM-LN*MN
По условиям задачи KL=27, MN=8, LN=x и KM=y
24²=27у-8х
576=27у-8х (2)
Решим систему уравнений:
{х*у=216
{576=27у-8х
Выразим значение х из первого уравнения: х=216/у
Подставим его во второе уравнение (метод подстановки):
576=27у-8х
576=27у-8*216/у
576=27у-1728/у (умножим все члены на у, чтобы избавиться от знаменателя)
576*у=27у²-1728
27у²-1728-576у=0
27у²—576у-1728=0
D=b²-4ac=(-576)²-4*27*(-1728)=331776+186624=518400 (√D= 720) у₁=(-b+√D)/2a=(-(-576)+720)/2*27=1296/54=24
у₂=(-b-√D)/2a=(-(-576)-720)/2*27=-144/27 – не подходит, т.к. х < 0
у=KM=24,
24х=216
х=LN=9
Р (ΔKMN)=KN+MN+KM=24+8+24=56
ответ: периметр треугольника KMN равен 56.