Задача решена Пользователем Рисадес Хорошист
Исправлена неточность в последнем действии.
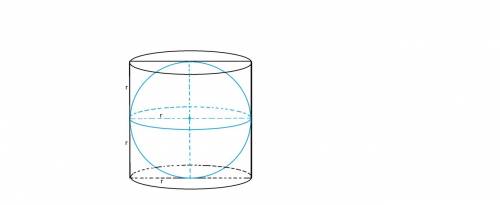
Шар может быть вписан в цилиндр только тогда, когда этот цилиндр правильный, т.е. когда его осевое сечение является квадратом.
Радиус основания цилиндра равен радиусу шара и равен r.
Высота цилиндра равна диаметру основания и равна 2 r.
Полная площадь поверхности складывается из площади двух оснований и площади боковой поверхности:
2*πr² + 2πr*2r = 6πr²
Площадь шара = 4πr²
Площадь цилиндра больше площади шара в
6πr² : 4πr² = 1,5 (раза)
Площадь полной поверхности шара
111 : 1,5 = 74 ( единиц площади)
Объяснение:
I)Найдите гипотенузу прямоугольного треугольника, если его катеты равны 1) 10см и 24см 2) 3см и 5 см.
По Пифагору: 1) с = √(10²+24²) = 26 см. 2) с = √(3²+5²) = √34 см.
II) Найдите катет прямоугольного треугольника, если его гипотенуза и второй катет соответсвенно равны 1) 26см и 10см 2)8см и 2см
По Пифагору: 1) b = √(26²-10²) = 24 см. 2) b = √(8²-2²) = 2√15 см.
III) Диагональ прямоугольника равна 34см. найдите стороны прямоугольника, если их длины относятся как 15:8
Диагональ прямоугольника делит его на два прямоугольных треугольника., катеты которых (стороны прямоугольника) относятся как 15:8, а гипотенуза равна 34 см. Тогда по Пифагору имеем:
34² = (15х)² + (8х)² = 289х² => x = √(34²/289) =34/17 = 2см.
Стороны прямоугольника равны две по 15·2 = 30см и две
по 8·2 = 16 см.
IV) Ошибка в условии. Высота треугольника не может быть равной боковой стороне. Решение при условии: В равнобедренном треугольнике ABC AB=СB=12см, выота BD=8см. Найдите основание AC треугольника.
Высота равнобедренного треугольника, проведенная к его основанию, является и медианой, то есть AD = DC. По Пифагору; AD = √(АВ²-BD²) = √(12²-8²) = 4√5 см.
AC = 2·AD = 2·4√5 = 8√5 см.
түзу деп те аталады.
Объяснение:
Сәуле деген бір нүктеден түзу шексіз кететін сызық. Оның басы бар шегі жоқ.